Which Is The Graph Of Linear Inequality X 2y 12
Breaking News Today
Jun 06, 2025 · 5 min read
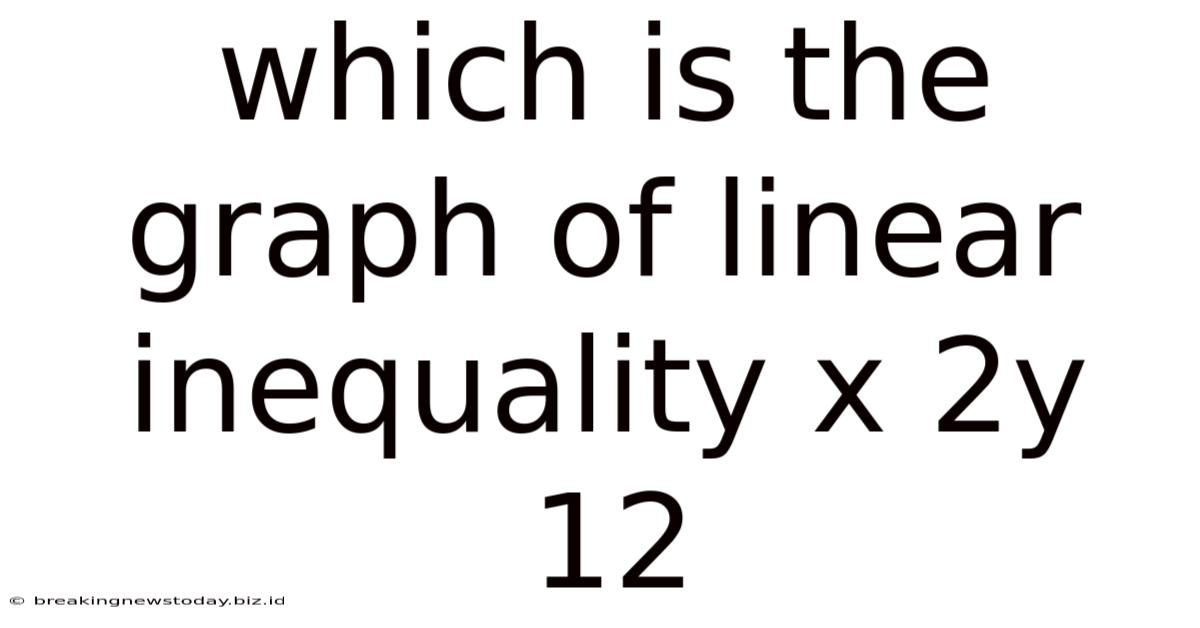
Table of Contents
Which is the Graph of Linear Inequality x + 2y ≤ 12? A Comprehensive Guide
Understanding linear inequalities is crucial for various mathematical applications, from optimization problems to analyzing relationships between variables. This article delves into the specifics of graphing the linear inequality x + 2y ≤ 12, explaining the process step-by-step and providing valuable insights into interpreting the resulting graph. We’ll also explore related concepts and techniques to solidify your understanding.
Understanding Linear Inequalities
A linear inequality is a mathematical statement that compares two expressions using inequality symbols such as ≤ (less than or equal to), ≥ (greater than or equal to), < (less than), or > (greater than). Unlike linear equations, which have a single solution, linear inequalities represent a range of solutions. The inequality x + 2y ≤ 12 signifies all points (x, y) where the expression x + 2y is less than or equal to 12.
Steps to Graph x + 2y ≤ 12
Graphing linear inequalities involves several key steps:
1. Treat it as an Equation:
First, treat the inequality as an equation: x + 2y = 12. This allows us to find the boundary line of the inequality's solution region.
2. Find the x and y-intercepts:
To graph the boundary line, find its intercepts.
- x-intercept: Set y = 0 and solve for x:
x + 2(0) = 12, which givesx = 12. This gives us the point (12, 0). - y-intercept: Set x = 0 and solve for y:
0 + 2y = 12, which givesy = 6. This gives us the point (0, 6).
Plot these two points on the coordinate plane.
3. Draw the Line:
Connect the x-intercept (12, 0) and the y-intercept (0, 6) with a straight line. Crucially, because our inequality includes "≤" (less than or equal to), the line should be solid. This indicates that points on the line are included in the solution set. If the inequality was < or >, the line would be dashed, showing that points on the line are not included.
4. Determine the Shaded Region:
This is the most important step. To determine which side of the line represents the solution to the inequality x + 2y ≤ 12, we need to test a point. The easiest point to test is the origin (0, 0).
Substitute the coordinates (0, 0) into the inequality: 0 + 2(0) ≤ 12. This simplifies to 0 ≤ 12, which is true.
Since the inequality is true for (0, 0), the region containing the origin is the solution region. Therefore, shade the area below the line.
5. The Complete Graph:
Your complete graph will show a solid line connecting (12, 0) and (0, 6), with the region below the line shaded. This shaded region represents all the points (x, y) that satisfy the inequality x + 2y ≤ 12.
Interpreting the Graph
The shaded region on the graph visually represents the infinite set of solutions for the inequality x + 2y ≤ 12. Any point within this shaded area, including points on the solid line, satisfies the condition that x + 2y is less than or equal to 12. Points outside the shaded region do not satisfy this condition.
Alternative Methods for Graphing
While the intercept method is straightforward, other methods can be used to graph linear inequalities, especially when dealing with more complex inequalities or those that don't easily provide integer intercepts.
1. The Slope-Intercept Form:
Rewrite the inequality in slope-intercept form (y ≤ mx + b), where 'm' is the slope and 'b' is the y-intercept. For x + 2y ≤ 12, we can rearrange it to:
2y ≤ -x + 12
y ≤ (-1/2)x + 6
This clearly shows the slope is -1/2 and the y-intercept is 6. You can use this information to plot the line and determine the shaded region as described above.
2. Using Test Points:
If the intercept method or slope-intercept form is inconvenient, choose any point not on the line. Substitute its coordinates into the inequality. If the inequality is true, shade the region containing that point. If false, shade the opposite region.
Solving Systems of Linear Inequalities
In real-world applications, you often encounter systems of linear inequalities—multiple inequalities that must be satisfied simultaneously. To graph a system, follow these steps:
- Graph each inequality individually, using the methods described above. Pay attention to whether the lines are solid or dashed.
- Identify the region where all the shaded regions overlap. This overlapping region represents the solution to the system of inequalities.
For example, consider the system:
x + 2y ≤ 12
x ≥ 0
y ≥ 0
Graphing these individually and finding the overlapping region would represent the solution set for this system. This type of system is often used to model constraints in linear programming problems.
Applications of Linear Inequalities
Linear inequalities are fundamental in many fields:
- Linear Programming: Used extensively in operations research to optimize resource allocation, production scheduling, and other logistical problems. The feasible region, representing all possible solutions that satisfy the constraints, is defined by a system of linear inequalities.
- Economics: Analyzing budget constraints, production possibilities, and consumer behavior often involves linear inequalities.
- Computer Graphics: Shading and rendering techniques utilize inequalities to determine which parts of a scene are visible and how light interacts with surfaces.
- Engineering: Designing structures and systems often involves satisfying multiple constraints expressed as inequalities.
Common Mistakes to Avoid
Several common mistakes can lead to incorrect graphs:
- Incorrectly drawing the boundary line: Carefully plot the intercepts and ensure the line is solid or dashed as appropriate.
- Shading the wrong region: Always test a point to determine the correct region to shade. Using the origin (0, 0) is usually the easiest, unless it lies on the line itself, in which case you need to choose a different test point.
- Not considering all constraints: When graphing systems of inequalities, ensure that you consider the intersection of all the shaded regions.
Conclusion
Graphing linear inequalities, particularly x + 2y ≤ 12, involves a systematic approach that combines algebraic manipulation with geometric representation. Understanding this process is critical for various mathematical and real-world applications. By mastering these techniques and avoiding common pitfalls, you can confidently analyze and solve problems involving linear inequalities and systems of linear inequalities. Remember to practice regularly to reinforce your understanding and improve your skills in graphical representation of mathematical concepts.
Latest Posts
Latest Posts
-
A Car Company Claims That The Lifetime Of Its Batteries
Jun 07, 2025
-
Place The Following Steps Of Retail Floral Processing In Order
Jun 07, 2025
-
Which Of These Best Characterizes The Jazz Age
Jun 07, 2025
-
According To The Monk Why Does Fortune Abandon People
Jun 07, 2025
-
A Food Worker Notices Several Boxes With Chew
Jun 07, 2025
Related Post
Thank you for visiting our website which covers about Which Is The Graph Of Linear Inequality X 2y 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.