Which Model Represents The Factors Of 4x2-9
Breaking News Today
Jun 08, 2025 · 5 min read
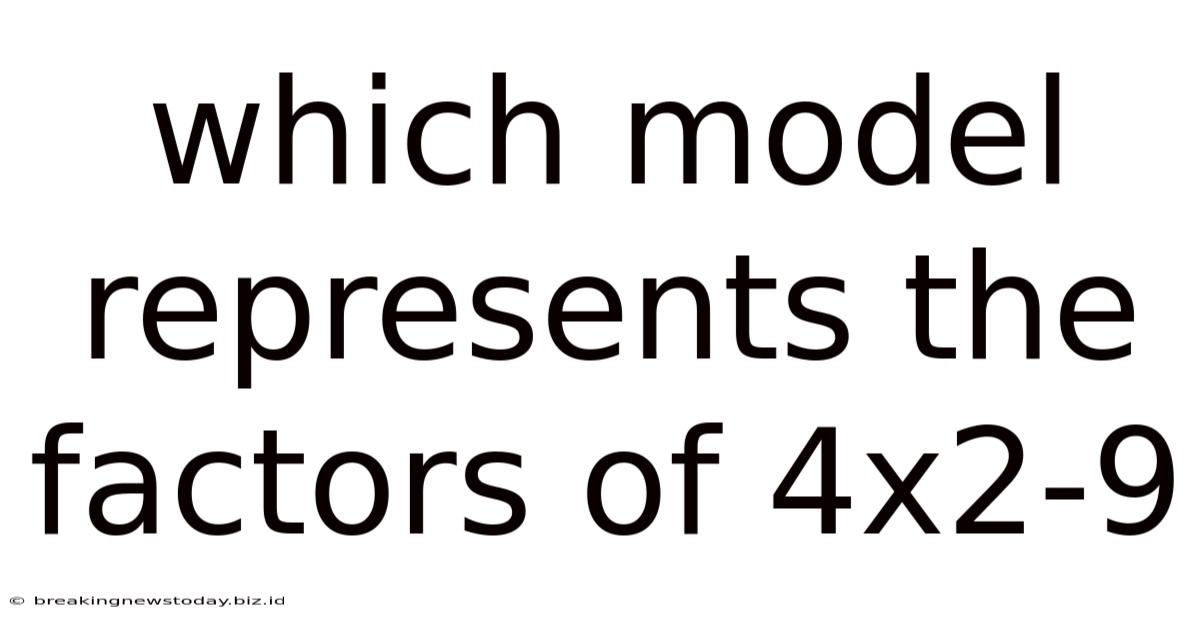
Table of Contents
Which Model Represents the Factors of 4x² - 9? A Deep Dive into Quadratic Expressions
The seemingly simple algebraic expression 4x² - 9 presents a fascinating opportunity to explore fundamental concepts in algebra, specifically factoring quadratic expressions and understanding their underlying models. This article will delve deep into the various ways we can represent the factors of 4x² - 9, examining different models and techniques, and highlighting their practical applications.
Understanding Quadratic Expressions
Before we tackle the factorization of 4x² - 9, let's establish a solid understanding of quadratic expressions. A quadratic expression is a polynomial of degree two, meaning the highest power of the variable (in this case, x) is 2. It generally takes the form ax² + bx + c, where a, b, and c are constants, and 'a' is not equal to zero. Our expression, 4x² - 9, is a special case of a quadratic expression where b = 0. This simplifies the factoring process considerably.
Method 1: Difference of Squares
The most straightforward approach to factoring 4x² - 9 involves recognizing it as a difference of squares. A difference of squares is an expression in the form a² - b², which can always be factored as (a + b)(a - b).
In our case, 4x² can be written as (2x)², and 9 can be written as 3². Therefore, 4x² - 9 can be expressed as (2x)² - 3². Applying the difference of squares formula, we get:
(2x + 3)(2x - 3)
This is the factored form of 4x² - 9. This model visually represents the expression as the product of two binomials, each containing a term with x and a constant term. This method is efficient and readily applicable to many similar quadratic expressions.
Method 2: Using the Quadratic Formula (Though not the most efficient here)
While the difference of squares method is the most elegant and efficient for 4x² - 9, we can also use the quadratic formula, a more general approach for solving quadratic equations. The quadratic formula solves for the roots (or zeros) of a quadratic equation of the form ax² + bx + c = 0:
x = [-b ± √(b² - 4ac)] / 2a
In our case, the equation is 4x² - 9 = 0, so a = 4, b = 0, and c = -9. Substituting these values into the quadratic formula:
x = [0 ± √(0² - 4 * 4 * -9)] / (2 * 4) x = ± √(144) / 8 x = ± 12 / 8 x = ± 3/2
This gives us the roots x = 3/2 and x = -3/2. These roots can be used to construct the factored form. Since the roots are α and β, the factored form is a(x - α)(x - β). In this case:
4(x - 3/2)(x + 3/2) = 2(x - 3/2) * 2(x + 3/2) = (2x - 3)(2x + 3)
This method, while functional, is unnecessarily complex for this particular problem. The difference of squares method is far more efficient.
Method 3: Graphical Representation – Visualizing the Factors
We can visualize the factors of 4x² - 9 through a graphical representation. The expression 4x² - 9 represents a parabola. The x-intercepts of this parabola correspond to the roots of the equation 4x² - 9 = 0. These x-intercepts are the points where the parabola intersects the x-axis.
By plotting the graph of y = 4x² - 9, we observe that the parabola intersects the x-axis at x = 3/2 and x = -3/2. These points correspond directly to the roots we found using the quadratic formula, and therefore, directly lead us back to the factors (2x + 3) and (2x - 3). This graphical model provides a visual interpretation of the roots and factors.
Applications and Significance
Understanding the factorization of quadratic expressions like 4x² - 9 has numerous applications in various fields:
1. Solving Quadratic Equations:
Factoring allows us to easily solve quadratic equations. Setting the factored form (2x + 3)(2x - 3) equal to zero and solving for x gives us the roots, as previously shown.
2. Calculus:
In calculus, factoring plays a crucial role in finding derivatives and integrals. Simplifying expressions through factoring makes these calculations more manageable.
3. Physics and Engineering:
Quadratic equations and their solutions are frequently encountered in physics and engineering problems, such as projectile motion, oscillations, and electrical circuits. The ability to factor quadratic expressions is essential for solving these problems.
4. Computer Science:
Algorithms in computer science often involve solving quadratic equations. Efficient factoring techniques contribute to the optimization of these algorithms.
Expanding the Concept: Beyond 4x² - 9
The techniques used to factor 4x² - 9 are applicable to a broader class of quadratic expressions. Understanding the difference of squares method is crucial for factoring expressions like:
- x² - 16: (x + 4)(x - 4)
- 9x² - 25: (3x + 5)(3x - 5)
- 100x² - 49: (10x + 7)(10x - 7)
These examples all share the common structure of a perfect square minus another perfect square, enabling the straightforward application of the difference of squares formula.
Conclusion: Choosing the Right Model
The choice of model for representing the factors of 4x² - 9 depends on the context and the desired outcome. While the difference of squares method is the most efficient and direct approach for this specific expression, understanding the quadratic formula and the graphical representation provides deeper insight into the underlying mathematical concepts. Regardless of the chosen model, mastering the factorization of quadratic expressions is fundamental to success in algebra and its various applications. The ability to efficiently factor these expressions not only aids in solving equations but also provides a crucial building block for more advanced mathematical concepts. It emphasizes the importance of understanding the underlying principles and applying the most efficient methods for a given problem. Remember, practice is key! The more you work with these types of problems, the more intuitive the factoring process will become.
Latest Posts
Latest Posts
-
4 03 Quiz Creating An American Mythology
Jun 08, 2025
-
Which Of The Following Is The Midsegment Of Abc
Jun 08, 2025
-
Which Statements Apply To Leasing A Car
Jun 08, 2025
-
A Lanyard Fall Arrest System Slows And Eventually Stops Descent
Jun 08, 2025
-
What Most Serves To Increase Tension In Both Stories
Jun 08, 2025
Related Post
Thank you for visiting our website which covers about Which Model Represents The Factors Of 4x2-9 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.