Which Points Are Solutions To The Linear Inequality Y 0.5x+2
Breaking News Today
Jun 04, 2025 · 5 min read
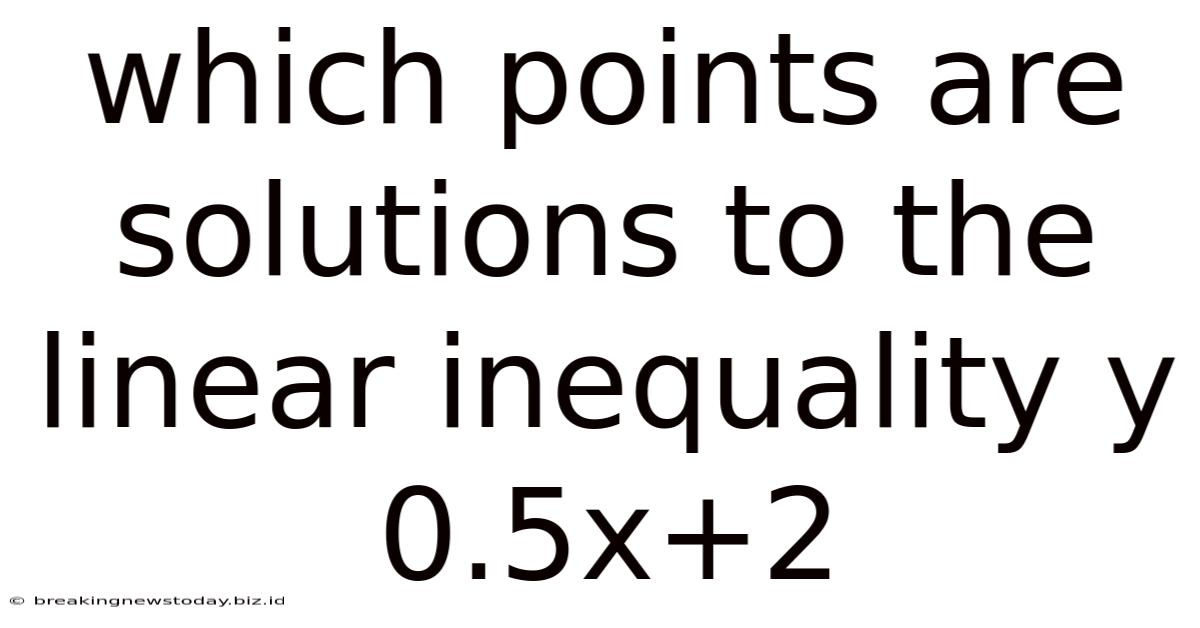
Table of Contents
Solutions to the Linear Inequality y > 0.5x + 2: A Comprehensive Guide
Understanding and visualizing linear inequalities is crucial for various mathematical applications. This article provides a comprehensive guide to finding and representing the solutions to the linear inequality y > 0.5x + 2. We'll explore different methods, including graphing, algebraic manipulation, and interpreting the results in context. By the end, you'll possess a solid understanding of how to solve and represent inequalities of this type.
Understanding the Inequality y > 0.5x + 2
The inequality y > 0.5x + 2 represents a half-plane in the Cartesian coordinate system. It signifies all points (x, y) where the y-coordinate is strictly greater than the value obtained by substituting the x-coordinate into the expression 0.5x + 2. The expression 0.5x + 2 itself represents a straight line with a slope of 0.5 and a y-intercept of 2.
Key Components:
y: The dependent variable. Its value depends on the value ofx.>: The inequality symbol, indicating "greater than." This means the solution includes points above the line.0.5x: The term representing the slope of the line. A slope of 0.5 indicates a gradual positive incline.+2: The y-intercept. The line crosses the y-axis at the point (0, 2).
Method 1: Graphical Representation
Graphing is the most intuitive way to visualize the solutions to this inequality. Follow these steps:
Step 1: Graph the Boundary Line
First, graph the line y = 0.5x + 2. This line serves as the boundary between the solution region and the non-solution region.
- Find two points: When x = 0, y = 2. When x = 2, y = 3. Plot these points (0, 2) and (2, 3) on the coordinate plane.
- Draw the line: Draw a straight line through these two points. Because the inequality is
>(strictly greater than), the line should be dashed, indicating that the points on the line itself are not part of the solution set.
Step 2: Shade the Solution Region
Since the inequality is y > 0.5x + 2, we need to shade the region above the line. This region represents all the points (x, y) that satisfy the inequality. Any point within the shaded region will make the inequality true.
Step 3: Verify a Test Point
To double-check your shading, select a test point not on the line. For example, let's test the point (0, 3). Substitute the coordinates into the inequality:
3 > 0.5(0) + 2
3 > 2
This is true, so the region containing (0, 3) should be shaded. If you had shaded the wrong region, this test would reveal the error.
Method 2: Algebraic Solutions
While graphing provides a visual representation, algebraic methods allow us to find specific solution points. This is particularly useful when dealing with complex inequalities or requiring precise numerical solutions.
Step 1: Isolate y
The inequality is already solved for y, which simplifies the process.
Step 2: Substitute x-values
Choose various values for x and substitute them into the inequality to find the corresponding values of y. Remember that y must be strictly greater than 0.5x + 2.
For example:
- If
x = 0,y > 0.5(0) + 2, soy > 2. Any value ofygreater than 2 will satisfy the inequality when x = 0. (e.g., (0, 2.1), (0, 10)) - If
x = 2,y > 0.5(2) + 2, soy > 3. (e.g., (2, 3.1), (2, 100)) - If
x = -2,y > 0.5(-2) + 2, soy > 1. (e.g., (-2, 1.1), (-2, 5))
Step 3: Expressing Solutions Algebraically
We can represent the solution set algebraically as: {(x, y) | y > 0.5x + 2}. This reads as "the set of all ordered pairs (x, y) such that y is greater than 0.5x + 2."
Method 3: Understanding the Contextual Implications
The practical applications of solving this inequality depend entirely on the context in which it arises. For example:
Scenario 1: Profit Analysis
Suppose x represents the number of units produced and y represents the profit. The inequality could model a scenario where the profit must exceed a certain threshold based on production levels. Finding solutions would involve determining production levels (x) that guarantee a sufficient profit (y).
Scenario 2: Resource Allocation
Imagine x represents hours spent on Task A and y represents hours spent on Task B. The inequality could define constraints on time allocation, ensuring that sufficient time is devoted to Task B relative to Task A. Solutions would represent feasible time allocations for both tasks.
Scenario 3: Temperature and Pressure
In scientific contexts, x and y could represent physical quantities like temperature and pressure. The inequality might describe a condition under which a particular chemical reaction proceeds, allowing us to determine suitable temperature and pressure ranges.
Advanced Considerations and Extensions
Compound Inequalities
The inequality y > 0.5x + 2 can be combined with other inequalities to create a system of inequalities that defines a more complex solution region. For example, adding the constraint x ≥ 0 would limit the solution to the first quadrant of the coordinate plane.
Nonlinear Inequalities
While this article focuses on linear inequalities, similar principles apply to nonlinear inequalities involving curves rather than straight lines. The methods for solving remain similar, involving graphing the boundary curve and testing points to determine the solution region.
Applications in Linear Programming
Linear programming problems often involve finding optimal solutions within a region defined by a system of linear inequalities. Understanding how to solve individual inequalities forms a foundation for solving more complex linear programming problems.
Conclusion
Solving the linear inequality y > 0.5x + 2 involves understanding its components, employing graphical or algebraic techniques, and interpreting the results within the given context. Whether visualizing the solution region on a graph or identifying specific solution points algebraically, the process enhances comprehension of linear inequalities and their applications in various fields. By mastering these techniques, you build a strong foundation for tackling more complex mathematical problems and real-world scenarios. Remember to always check your solutions and consider the practical implications within the context of the problem. Practice solving different inequalities to solidify your understanding and improve your problem-solving skills.
Latest Posts
Latest Posts
-
Which Of The Following Are Realistic Consequences Of Plagiarism
Jun 05, 2025
-
Circle Two Addends To Add First Write The Sum 3 3 4
Jun 05, 2025
-
Correct See The Constitutional Basis Of Federalism L O 3 3
Jun 05, 2025
-
A Food Handler May Chew Tobacco In Servsafe
Jun 05, 2025
-
Which Is A Strength Training Activity Sit Ups Tennis Hopscotch Jump Roping
Jun 05, 2025
Related Post
Thank you for visiting our website which covers about Which Points Are Solutions To The Linear Inequality Y 0.5x+2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.