Which Shows Two Triangles That Are Congruent By Aas
Breaking News Today
Mar 30, 2025 · 5 min read
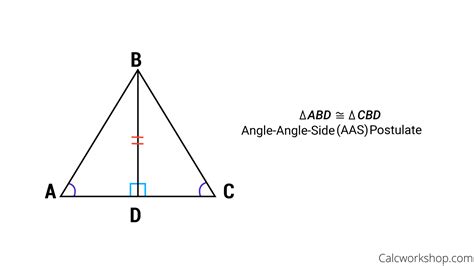
Table of Contents
Proving Triangle Congruence: A Deep Dive into AAS
Understanding triangle congruence is fundamental in geometry. It allows us to establish relationships between different triangles and to solve problems involving lengths, angles, and areas. One of the key postulates used to prove congruence is the Angle-Angle-Side (AAS) postulate. This article will delve deep into the AAS postulate, providing a comprehensive understanding of its application, proving its validity, and showcasing examples with detailed explanations. We'll also explore how AAS differs from other congruence postulates, highlighting its strengths and limitations.
Understanding the AAS Postulate
The AAS postulate states that if two angles and a non-included side of one triangle are congruent to two angles and the corresponding non-included side of another triangle, then the triangles are congruent. Let's break this down:
- Two Angles: We need two corresponding angles from each triangle to be equal in measure.
- Non-included Side: The side we're comparing must not be between the two angles we've already established as congruent. It's the side that connects one of the angles to a vertex outside of the pair of angles.
This seemingly specific requirement is crucial. It ensures that there is only one possible way to construct a triangle given this information, guaranteeing congruence.
Visualizing AAS
Imagine two triangles, ΔABC and ΔDEF. To prove they're congruent using AAS, we need to demonstrate:
- ∠A ≅ ∠D
- ∠B ≅ ∠E
- BC ≅ EF
Notice that side BC is not included between angles A and B, and similarly, EF is not included between angles D and E. This satisfies the non-included side condition.
(Insert image here: Two triangles, ΔABC and ΔDEF, clearly labeled with congruent angles and non-included sides highlighted. The image should visually represent the AAS criteria.)
Proving the Validity of AAS
While AAS is often presented as a postulate (a statement accepted as true without proof), its validity can be derived from other established postulates or theorems. The most common approach is to prove AAS using the ASA (Angle-Side-Angle) postulate, which is often considered a foundational postulate in geometry.
Proof using ASA:
Let's assume we have two triangles, ΔABC and ΔDEF, that satisfy the AAS condition:
-
Given: ∠A ≅ ∠D, ∠B ≅ ∠E, BC ≅ EF.
-
Find the third angle: In any triangle, the sum of angles is 180°. Therefore, ∠C = 180° - ∠A - ∠B, and ∠F = 180° - ∠D - ∠E. Since ∠A ≅ ∠D and ∠B ≅ ∠E, it follows that ∠C ≅ ∠F.
-
Apply ASA: Now we have ∠A ≅ ∠D, BC ≅ EF (the side between angles A and C and D and F respectively), and ∠C ≅ ∠F. This satisfies the ASA postulate.
-
Conclusion: Since the triangles satisfy ASA, which is a proven postulate, they are congruent. Therefore, the AAS postulate is valid.
Distinguishing AAS from other Congruence Postulates
Several postulates and theorems can be used to prove triangle congruence. Understanding the nuances between them is vital:
- SSS (Side-Side-Side): If all three sides of one triangle are congruent to the corresponding sides of another triangle, the triangles are congruent.
- SAS (Side-Angle-Side): If two sides and the included angle of one triangle are congruent to two sides and the included angle of another triangle, the triangles are congruent.
- ASA (Angle-Side-Angle): If two angles and the included side of one triangle are congruent to two angles and the included side of another triangle, the triangles are congruent.
- AAS (Angle-Angle-Side): As discussed above, this involves two angles and a non-included side.
- HL (Hypotenuse-Leg - Right Triangles Only): If the hypotenuse and a leg of one right triangle are congruent to the hypotenuse and a leg of another right triangle, the triangles are congruent.
The key difference between AAS and the others lies in the placement of the congruent side relative to the congruent angles. In AAS, the congruent side is not included between the congruent angles. This distinction is crucial when analyzing geometric problems.
Worked Examples: Applying AAS
Let's illustrate the application of the AAS postulate with several examples:
Example 1: Simple Application
(Insert image here: Two triangles, ΔPQR and ΔXYZ, with angles and side lengths clearly marked, showing congruence using AAS.)
In ΔPQR and ΔXYZ:
- ∠P ≅ ∠X = 70°
- ∠Q ≅ ∠Y = 60°
- QR ≅ YZ = 5cm
Therefore, ΔPQR ≅ ΔXYZ by AAS.
Example 2: More Complex Scenario
This example involves a bit more deduction:
(Insert image here: A more complex diagram involving two triangles within a larger figure, requiring some steps to identify congruent angles and sides to apply AAS.)
Let’s say we have a diagram with two intersecting lines forming angles. We need to demonstrate that two triangles within this figure are congruent using AAS. We might need to use properties of vertical angles, alternate interior angles, or supplementary angles to establish congruence before directly applying AAS. This example emphasizes the importance of combining different geometric concepts to prove congruence.
Example 3: Real-world Application
Imagine a surveyor measuring the distance across a river. They can use the AAS postulate to indirectly measure the distance by setting up two triangles with congruent angles and one measured side. This application demonstrates the practical utility of understanding triangle congruence in real-world scenarios.
(Insert image here: A simple diagram of a surveyor using triangles to measure the width of a river. Clearly mark congruent angles and known side.)
Limitations of AAS
While AAS is a powerful tool, it's important to recognize its limitations. It only applies to triangles. It cannot be used to prove congruence for other geometric shapes. Also, the identification of congruent angles and sides is crucial. Inaccurate measurements or incorrect assumptions can lead to an erroneous conclusion.
Conclusion
The AAS postulate is a valuable tool in proving triangle congruence. Its validity rests upon the foundational principles of geometry and can be derived from other established postulates. By understanding its application and limitations, and by comparing it to other congruence postulates, we can effectively utilize AAS to solve various geometric problems and appreciate its significance in different fields, including surveying and engineering. Remember to always carefully examine the given information and ensure all conditions of AAS are met before applying the postulate.
Latest Posts
Latest Posts
-
Nurse Logic Knowledge And Clinical Judgment Beginner
Apr 01, 2025
-
First 36 Elements On The Periodic Table
Apr 01, 2025
-
A Computer Training Business Needs To Hire A Consultant
Apr 01, 2025
-
All Results Have An Obvious Link To A Landing Page
Apr 01, 2025
-
Identifying And Safeguarding Pii V4 Test Out Answers
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about Which Shows Two Triangles That Are Congruent By Aas . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
