Which Statement Is True About The Graphed Function
Breaking News Today
Mar 24, 2025 · 7 min read
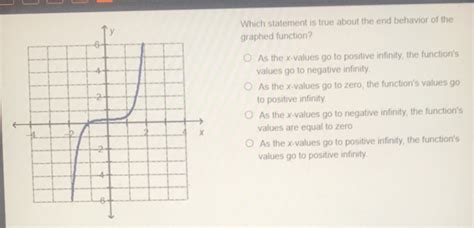
Table of Contents
Which Statement is True About the Graphed Function? A Comprehensive Guide
Analyzing graphs of functions is a fundamental skill in mathematics, crucial for understanding various concepts across algebra, calculus, and beyond. This article delves deep into interpreting graphed functions, exploring various characteristics and how to determine the truthfulness of statements about them. We'll cover key features like domain and range, intercepts, asymptotes, increasing and decreasing intervals, relative extrema, concavity, and inflection points. Understanding these elements allows you to accurately analyze a graph and ascertain the validity of any given statement.
Understanding Key Features of Graphed Functions
Before we can determine the truthfulness of statements about a graphed function, we must be comfortable identifying its key features. Let's explore these features in detail:
1. Domain and Range
The domain of a function is the set of all possible input values (x-values) for which the function is defined. The range is the set of all possible output values (y-values) the function can produce. Visually inspecting a graph, the domain is the span of x-values the graph covers, and the range is the span of y-values.
Example: If a graph stretches from x = -2 to x = 5, the domain is typically expressed as [-2, 5] or -2 ≤ x ≤ 5. Similarly, if the y-values range from y = 1 to y = 7, the range is [1, 7] or 1 ≤ y ≤ 7. Note that parentheses ( ) indicate an open interval (excluding the endpoint), while brackets [ ] indicate a closed interval (including the endpoint).
2. Intercepts
x-intercepts (also known as roots or zeros) are the points where the graph intersects the x-axis (where y = 0). y-intercepts are the points where the graph intersects the y-axis (where x = 0). Identifying these points is crucial for understanding the behavior of the function.
Example: If a graph intersects the x-axis at x = 1 and x = 4, then the x-intercepts are (1, 0) and (4, 0). If it intersects the y-axis at y = 2, the y-intercept is (0, 2).
3. Asymptotes
Asymptotes are lines that a graph approaches but never actually touches. There are three main types:
- Vertical Asymptotes: Occur where the function approaches positive or negative infinity as x approaches a specific value. They often indicate values where the function is undefined (e.g., division by zero).
- Horizontal Asymptotes: Occur as x approaches positive or negative infinity. They represent the limiting behavior of the function.
- Oblique (Slant) Asymptotes: Occur when the degree of the numerator is one greater than the degree of the denominator in a rational function.
Example: A graph might have a vertical asymptote at x = 2, indicating the function is undefined at x = 2. It might have a horizontal asymptote at y = 3, indicating the function approaches 3 as x approaches infinity.
4. Increasing and Decreasing Intervals
A function is increasing on an interval if its y-values increase as its x-values increase. It's decreasing if its y-values decrease as its x-values increase. These intervals are essential for understanding the overall trend of the function.
Example: If a graph is rising from x = -1 to x = 2, the function is increasing on the interval (-1, 2). If it's falling from x = 2 to x = 5, it's decreasing on (2, 5).
5. Relative Extrema
Relative extrema (also known as local extrema) are points where the function reaches a local maximum or minimum value. A relative maximum is a peak, while a relative minimum is a valley. These points often signify turning points in the graph.
Example: A graph might have a relative maximum at (1, 4) and a relative minimum at (3, 1).
6. Concavity and Inflection Points
The concavity of a function describes the curvature of its graph. A function is concave up if it curves upwards (like a smile), and concave down if it curves downwards (like a frown). An inflection point is a point where the concavity changes (from concave up to concave down or vice versa).
Example: A graph might be concave up on the interval (0, 2) and concave down on (2, 4), with an inflection point at x = 2.
Analyzing Statements About Graphed Functions
Now that we've covered the key features, let's look at how to analyze statements about graphed functions. The process involves carefully examining the graph and comparing its features to the information provided in the statement.
Example Statements and Analysis:
Let's consider a hypothetical graph of a function. We'll evaluate several statements about it:
Statement 1: The function has a y-intercept at (0, 2).
Analysis: Examine the graph at x = 0. If the graph intersects the y-axis at y = 2, the statement is true. Otherwise, it's false.
Statement 2: The function is increasing on the interval (-∞, 1).
Analysis: Check the graph's behavior to the left of x = 1. If the y-values consistently increase as x increases in this interval, the statement is true. If the graph decreases or remains constant at any point in this interval, the statement is false.
Statement 3: The function has a relative minimum at x = 3.
Analysis: Look for a "valley" in the graph around x = 3. If a local minimum occurs at x = 3 (meaning the function value at x=3 is smaller than values around it), the statement is true; otherwise, it's false.
Statement 4: The function has a vertical asymptote at x = -2.
Analysis: Check for a vertical line at x = -2 that the graph approaches but doesn't cross. If present, the statement is true; otherwise, it's false.
Statement 5: The domain of the function is all real numbers.
Analysis: Examine the graph's extent along the x-axis. If the graph extends infinitely in both directions without any breaks or gaps, the statement is true. If there are any gaps or restrictions on x-values, such as asymptotes or holes, then the statement is false.
Statement 6: The range of the function is (-∞, 4].
Analysis: Inspect the graph's vertical extent. If the graph spans all y-values less than or equal to 4, the statement is true. Otherwise, it is false. Note the use of a square bracket ] to denote inclusion of the value 4.
Statement 7: The function is concave up on the interval (2, 5).
Analysis: On the interval (2,5) observe the curvature of the graph. If the graph curves upwards like a smile throughout the interval (2,5), the statement is true. If the graph is concave down or changes concavity within that interval, the statement is false.
Statement 8: The function has an inflection point at x = 2.
Analysis: Look for a change in concavity at x = 2. If the concavity switches from concave up to concave down (or vice versa) at x = 2, the statement is true. If there’s no change in concavity, or the concavity doesn't change at x = 2, then the statement is false.
Advanced Considerations
For more complex functions, you might encounter statements involving limits, derivatives, or integrals. In such cases, a deeper understanding of calculus is required. However, the fundamental principles of analyzing the graph remain the same. Always break down complex statements into smaller, manageable parts, relating each part to specific features of the graph. Carefully examine the graph for discontinuities, turning points, and changes in concavity to accurately assess the truthfulness of any statement.
Practical Application and Conclusion
The ability to accurately analyze statements about graphed functions is essential in many fields, including engineering, physics, economics, and computer science. Understanding graphical representation of data and the underlying mathematical relationships allows for effective problem-solving and informed decision-making. By mastering the techniques outlined in this article, you'll enhance your mathematical skills and improve your ability to interpret and analyze graphical data effectively. Remember to always systematically examine the graph's key features and compare them to the statement's claims to reach accurate conclusions. Practice makes perfect – the more graphs you analyze, the more proficient you'll become.
Latest Posts
Latest Posts
-
Over The Past Decades The Turnout Of Minority Voters Has
Mar 29, 2025
-
Cyber Awareness Challenge 2025 Knowledge Check Answers
Mar 29, 2025
-
Which Assessment Finding Is Consistent With Right Sided Heart Failure
Mar 29, 2025
-
Which Of The Following Is A Result Of Natural Erosion
Mar 29, 2025
-
Which Of These Statements Best Describes A Suicide Cluster
Mar 29, 2025
Related Post
Thank you for visiting our website which covers about Which Statement Is True About The Graphed Function . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
