Which System Of Linear Inequalities Is Represented By The Graph
Breaking News Today
Mar 30, 2025 · 5 min read
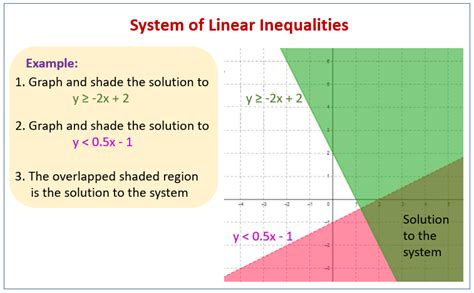
Table of Contents
Which System of Linear Inequalities is Represented by the Graph? A Comprehensive Guide
Understanding how to interpret graphs representing systems of linear inequalities is crucial in algebra and various applications. This comprehensive guide will walk you through the process, equipping you with the skills to identify the correct system from a given graphical representation. We'll cover key concepts, step-by-step procedures, and practical examples to solidify your understanding. By the end, you'll be confident in analyzing such graphs and translating them into their algebraic counterparts.
Understanding Linear Inequalities and Their Graphs
Before diving into systems, let's review the fundamentals of linear inequalities. A linear inequality is a mathematical statement comparing two expressions using inequality symbols: < (less than), > (greater than), ≤ (less than or equal to), or ≥ (greater than or equal to). For example, y > 2x + 1 is a linear inequality.
When graphed, a linear inequality forms a region on the coordinate plane.
-
Solid Line vs. Dashed Line: If the inequality includes "or equal to" (≤ or ≥), the boundary line is solid, indicating that points on the line are part of the solution set. If the inequality is strictly less than (<) or greater than (>), the boundary line is dashed, meaning points on the line are not included in the solution set.
-
Shading: The region that satisfies the inequality is shaded. To determine which side to shade, test a point (usually (0,0) if it's not on the line) in the inequality. If the point makes the inequality true, shade the region containing the point; otherwise, shade the other region.
Systems of Linear Inequalities: Where the Magic Happens
A system of linear inequalities involves two or more linear inequalities considered simultaneously. The solution to the system is the region where the solution sets of all the inequalities overlap. This overlapping region is often a polygon (or unbounded region).
Deciphering the Graph: A Step-by-Step Approach
Let's break down the process of identifying the system of linear inequalities represented by a graph:
Step 1: Identify the Boundary Lines
Carefully examine the graph. Count the number of boundary lines. Each line represents a linear inequality. Note whether each line is solid or dashed.
Step 2: Determine the Equation of Each Line
For each line, find its equation. You can do this by:
-
Finding the slope and y-intercept: If the y-intercept and at least one other point are easily identifiable from the graph, you can determine the slope (m) using the formula
m = (y2 - y1) / (x2 - x1)and then use the slope-intercept form:y = mx + b. -
Using two points: If you can identify two points on the line, use them to find the slope and then use the point-slope form:
y - y1 = m(x - x1)to find the equation. -
Using intercepts: If the x and y intercepts are easily visible, you can use the intercept form:
x/a + y/b = 1, where 'a' is the x-intercept and 'b' is the y-intercept.
Step 3: Determine the Inequality Symbol
For each line, determine whether the inequality symbol is <, >, ≤, or ≥.
-
Shading: Observe which side of the line is shaded. If the region above the line is shaded, the inequality involves '>' or '≥'. If the region below the line is shaded, the inequality involves '<' or '≤'.
-
Solid vs. Dashed: A solid line indicates '≤' or '≥'; a dashed line indicates '<' or '>'.
Step 4: Check the Overlapping Region
The solution to the system of inequalities is the region where the shaded areas of all the individual inequalities overlap. Ensure that the inequalities you've derived correctly represent this overlapping region. If it doesn't match, you've made an error in one or more steps.
Step 5: Write the System of Inequalities
Once you have determined the equation and inequality symbol for each line, write the system of inequalities. This is your final answer.
Example: Putting it All Together
Let's say a graph shows two lines:
- Line 1: A solid line passing through (0, 2) and (1, 0). The region below the line is shaded.
- Line 2: A dashed line passing through (0, -1) and (2, 1). The region above the line is shaded.
Step 1: Two boundary lines.
Step 2:
- Line 1: The slope is (0 - 2) / (1 - 0) = -2. The y-intercept is 2. Therefore, the equation is y = -2x + 2.
- Line 2: The slope is (1 - (-1)) / (2 - 0) = 1. Using the point-slope form with (0,-1), we get y - (-1) = 1(x - 0), which simplifies to y = x - 1.
Step 3:
- Line 1: The line is solid, and the region below is shaded, so the inequality is y ≤ -2x + 2.
- Line 2: The line is dashed, and the region above is shaded, so the inequality is y > x - 1.
Step 4: The overlapping region is where y ≤ -2x + 2 and y > x - 1 simultaneously. Verify visually on the graph.
Step 5: The system of inequalities is:
y ≤ -2x + 2
y > x - 1
Advanced Considerations
-
Unbounded Regions: Some systems of inequalities result in unbounded regions – regions that extend infinitely in one or more directions.
-
No Solution: In some cases, the individual inequalities might not overlap, meaning there is no solution to the system.
-
More than Two Inequalities: The same principles apply when dealing with systems involving more than two inequalities. You simply need to repeat the steps for each additional line.
Practical Applications
Understanding systems of linear inequalities is essential in various fields:
- Operations Research: Optimizing resource allocation, production planning, and scheduling.
- Economics: Modeling supply and demand, budget constraints, and portfolio optimization.
- Computer Science: Linear programming and algorithm design.
- Engineering: Constraint satisfaction problems and design optimization.
Conclusion
Mastering the interpretation of graphs representing systems of linear inequalities is a valuable skill. By following the step-by-step process outlined above, you can confidently translate graphical representations into their algebraic counterparts, opening doors to deeper understanding and application in numerous fields. Remember to practice regularly to hone your skills and build your confidence in tackling increasingly complex problems. The more you practice, the more intuitive this process will become.
Latest Posts
Latest Posts
-
Selecciona La Palabra Que No Esta Relacionada
Apr 01, 2025
-
A Nurse Is Preparing To Administer Phenylephrine To A Client
Apr 01, 2025
-
When Performing The Jaw Thrust Maneuver On Patients With Suspected
Apr 01, 2025
-
A Firm Pursuing A Best Cost Provider Strategy
Apr 01, 2025
-
Es Donde Pones La Cabeza Cuando Duermes
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about Which System Of Linear Inequalities Is Represented By The Graph . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
