X 12y 210 And X 6y 90 Then X
Breaking News Today
Jun 04, 2025 · 4 min read
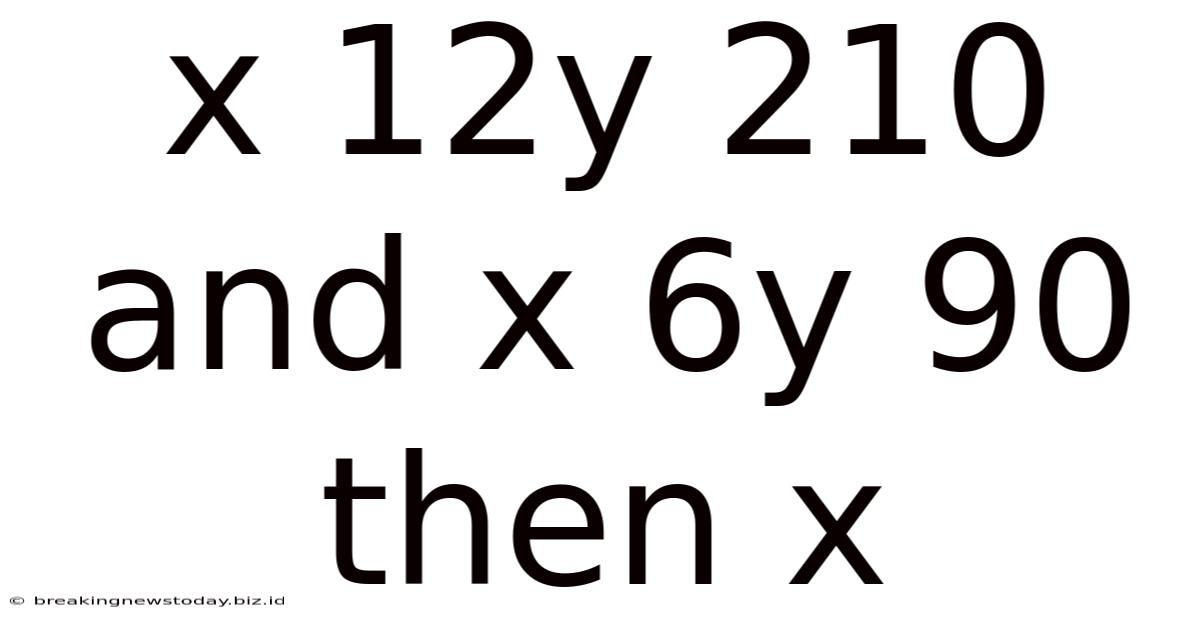
Table of Contents
Solving Simultaneous Equations: A Deep Dive into x + 12y = 210 and x + 6y = 90
This article will explore the process of solving simultaneous equations, focusing specifically on the system:
- x + 12y = 210
- x + 6y = 90
We'll delve into various methods, comparing their strengths and weaknesses, and ultimately determine the values of 'x' and 'y' that satisfy both equations. This problem is a classic example of a linear system, offering a great opportunity to understand fundamental algebraic concepts crucial for various fields, from mathematics and physics to economics and computer science.
Understanding Simultaneous Equations
Simultaneous equations are a set of two or more equations that contain two or more variables. The goal is to find the values of the variables that satisfy all equations simultaneously. In simpler terms, we're looking for the point(s) where the lines (or planes, in higher dimensions) represented by the equations intersect.
Our specific example, x + 12y = 210 and x + 6y = 90, represents two straight lines on a Cartesian plane. The solution to this system is the coordinates (x, y) of the point where these lines cross.
Methods for Solving Simultaneous Equations
Several methods exist for solving simultaneous equations. We'll explore three common techniques:
1. Elimination Method
The elimination method focuses on eliminating one variable by adding or subtracting the equations. This method is particularly effective when the coefficients of one variable in both equations are opposites or multiples of each other.
Let's apply this to our equations:
- x + 12y = 210 (Equation 1)
- x + 6y = 90 (Equation 2)
Notice that the coefficient of 'x' is the same in both equations. Subtracting Equation 2 from Equation 1 will eliminate 'x':
(x + 12y) - (x + 6y) = 210 - 90
This simplifies to:
6y = 120
Dividing both sides by 6, we find:
y = 20
Now, substitute the value of 'y' (20) back into either Equation 1 or Equation 2 to solve for 'x'. Let's use Equation 2:
x + 6(20) = 90
x + 120 = 90
x = 90 - 120
x = -30
Therefore, the solution to the simultaneous equations is x = -30 and y = 20.
2. Substitution Method
The substitution method involves solving one equation for one variable in terms of the other and then substituting this expression into the second equation.
Let's solve Equation 2 for 'x':
x = 90 - 6y
Now, substitute this expression for 'x' into Equation 1:
(90 - 6y) + 12y = 210
Simplify and solve for 'y':
90 + 6y = 210
6y = 120
y = 20
Substitute the value of 'y' back into the expression for 'x':
x = 90 - 6(20)
x = -30
Again, we arrive at the solution x = -30 and y = 20.
3. Graphical Method
The graphical method involves plotting both equations on a Cartesian plane. The point of intersection represents the solution to the simultaneous equations. While this method provides a visual representation of the solution, it's less precise than algebraic methods, especially when dealing with non-integer solutions.
To graph the equations, we can find two points for each line and connect them. For example:
Equation 1 (x + 12y = 210):
- If y = 0, then x = 210. Point (210, 0)
- If x = 0, then y = 210/12 = 17.5. Point (0, 17.5)
Equation 2 (x + 6y = 90):
- If y = 0, then x = 90. Point (90, 0)
- If x = 0, then y = 90/6 = 15. Point (0, 15)
Plotting these points and drawing the lines, you'll observe they intersect at (-30, 20), confirming our algebraic solutions.
Verification and Interpretation
It's crucial to verify the solution by substituting the values of 'x' and 'y' back into both original equations:
Equation 1: -30 + 12(20) = -30 + 240 = 210. Correct!
Equation 2: -30 + 6(20) = -30 + 120 = 90. Correct!
This confirms that x = -30 and y = 20 is the correct solution to the simultaneous equations. The interpretation depends on the context of the problem. If these equations represent a real-world scenario (e.g., cost and quantity in a business problem), the solution provides specific values for the relevant variables.
Expanding on the Concepts: Matrix Methods and Applications
For more complex systems of equations (with more variables), more sophisticated methods like matrix methods (e.g., Gaussian elimination, Cramer's rule) become necessary. These methods are particularly useful in computer programming and data analysis where efficiency in solving large systems is critical.
The ability to solve simultaneous equations is fundamental to numerous applications across diverse fields:
- Engineering: Analyzing circuits, structural mechanics, and fluid dynamics.
- Economics: Modeling supply and demand, optimizing resource allocation.
- Computer Science: Solving linear systems in computer graphics, machine learning, and optimization problems.
- Physics: Solving systems of forces, analyzing motion, and modeling various physical phenomena.
- Chemistry: Solving equilibrium problems and stoichiometry calculations.
Conclusion
Solving simultaneous equations, such as x + 12y = 210 and x + 6y = 90, is a cornerstone of algebra with widespread applications. This article has explored three primary methods – elimination, substitution, and graphical – showcasing their strengths and weaknesses. Understanding these methods is crucial for success in various academic and professional pursuits. Remember to always verify your solutions and consider the context of the problem to fully interpret the results. For larger systems, exploring matrix methods provides a powerful and efficient approach. The ability to confidently solve simultaneous equations is a testament to a solid foundation in mathematical problem-solving.
Latest Posts
Latest Posts
-
If A Stock Clerk Receives Six Shipments
Jun 05, 2025
-
The Graph Represents The Market For Breakfast Cereals
Jun 05, 2025
-
What Did The Detective Say To The Crook
Jun 05, 2025
-
Where Did The Granite Go On Saturday Night
Jun 05, 2025
-
What Makes The Figures In The Above Image Recognizably Korean
Jun 05, 2025
Related Post
Thank you for visiting our website which covers about X 12y 210 And X 6y 90 Then X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.