X Is The Midpoint Of Wy And Vz
Breaking News Today
Jun 05, 2025 · 5 min read
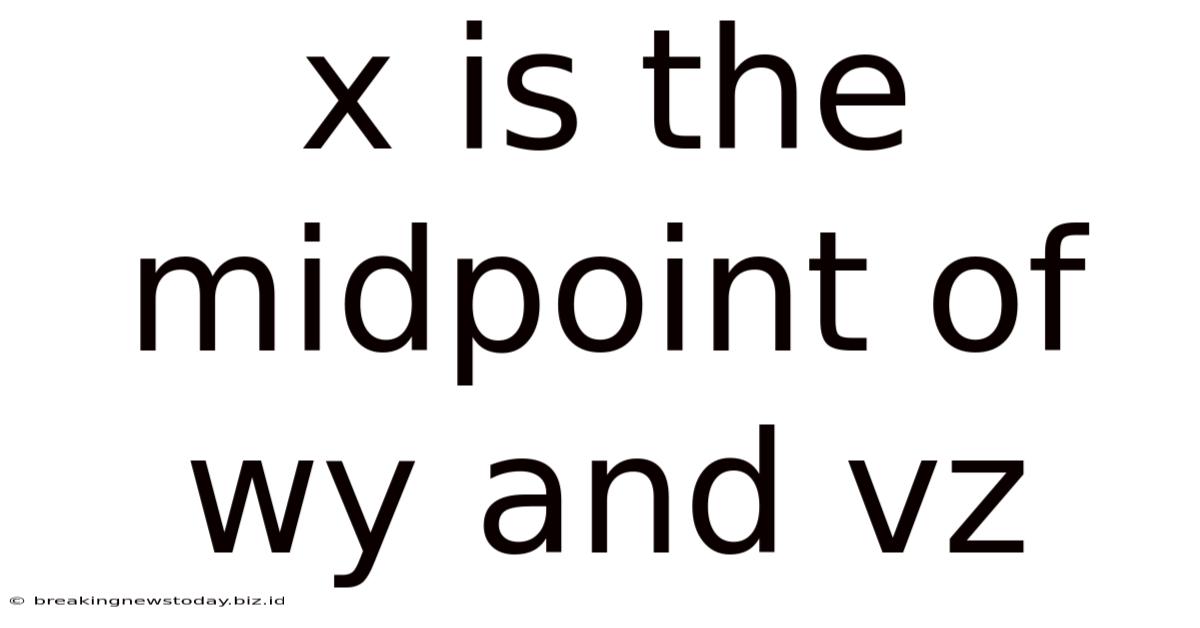
Table of Contents
X is the Midpoint of WY and VZ: Exploring Midpoint Theorems and Their Applications
This article delves into the fascinating world of geometry, specifically focusing on the concept of a midpoint and its implications within various geometric figures. We will explore the statement "X is the midpoint of WY and VZ" in detail, examining its significance, proving its validity under specific conditions, and showcasing its applications in problem-solving and advanced geometric concepts.
Understanding Midpoints
Before diving into the core concept, let's establish a firm understanding of what a midpoint is. A midpoint is a point that divides a line segment into two equal parts. In simpler terms, it's the exact middle point of a line segment. If we have a line segment AB, and X is the midpoint, then AX = XB. This seemingly simple concept forms the foundation for numerous theorems and applications in geometry.
Properties of Midpoints
Several key properties stem from the definition of a midpoint:
- Equal lengths: The distance from one endpoint of the segment to the midpoint is equal to the distance from the midpoint to the other endpoint.
- Bisecting the segment: The midpoint bisects the line segment, dividing it into two congruent segments.
- Coordinate calculation: If we have the coordinates of the endpoints of a line segment, we can easily calculate the coordinates of the midpoint using the midpoint formula: Midpoint = ((x₁ + x₂)/2, (y₁ + y₂)/2).
X as the Midpoint of WY and VZ: Exploring the Possibilities
The statement "X is the midpoint of WY and VZ" implies that X lies on both line segments WY and VZ, dividing each segment into two equal halves. This scenario presents several possibilities and implications, depending on the context:
Scenario 1: WY and VZ are intersecting line segments
If WY and VZ are two intersecting line segments, and X is their intersection point, then X could be the midpoint of both segments. However, this is not necessarily the case. The intersection of two line segments does not automatically imply that the intersection point is the midpoint of both.
Example: Consider two line segments that intersect at a point, but where the intersection point is closer to one end of each segment. This clearly demonstrates that intersection does not automatically imply midpoint.
Scenario 2: WY and VZ are diagonals of a parallelogram
If WY and VZ are the diagonals of a parallelogram, then their intersection point X is the midpoint of both diagonals. This is a fundamental property of parallelograms. The diagonals of a parallelogram bisect each other.
Proof: This property can be proven using various geometric principles, often involving congruent triangles and parallel lines. A common approach involves showing that triangles formed by the diagonals are congruent, leading to the conclusion that the diagonals bisect each other.
Scenario 3: WY and VZ are part of a specific geometric shape
Depending on the shape in which WY and VZ are embedded, the condition that X is the midpoint of both may or may not hold true. For instance, in certain quadrilaterals or other polygons, this condition might be a defining characteristic or a consequence of other properties.
Implications and Applications
The statement "X is the midpoint of WY and VZ" holds significant implications and has numerous applications across various areas of geometry and related fields:
1. Determining the lengths of segments
Knowing that X is the midpoint allows us to easily calculate the length of the segments. If we know the length of WX, we automatically know the length of XY (they are equal). Similarly, if we know the length of VX, we know the length of XZ.
2. Coordinate geometry
If the coordinates of W, Y, V, and Z are known, the coordinates of X can be calculated using the midpoint formula. Conversely, if the coordinates of X and one endpoint are known, the coordinates of the other endpoint can be determined. This is extremely useful in coordinate geometry problems.
3. Constructing geometric figures
The concept of midpoints is crucial in constructing various geometric figures accurately. For example, to construct a parallelogram, one can use the midpoints of the diagonals as a reference point.
4. Solving geometric problems
Many geometry problems rely on the properties of midpoints to solve them efficiently. These problems might involve proving congruency, calculating lengths, or finding areas of geometric shapes.
5. Advanced geometric concepts
The concept of midpoints extends to more advanced geometric concepts such as medians in triangles and centroids. A median of a triangle connects a vertex to the midpoint of the opposite side. The centroids, the point of intersection of the medians, has unique properties related to the center of mass of the triangle.
Further Exploration: Midpoint Theorem in Triangles
The midpoint theorem is a powerful result that directly relates to midpoints. The theorem states that the line segment joining the midpoints of two sides of a triangle is parallel to the third side and half its length.
Statement: Let's consider triangle ABC. If D and E are the midpoints of sides AB and AC respectively, then DE is parallel to BC and DE = (1/2)BC.
Proof: The proof of the midpoint theorem involves various geometric techniques such as congruent triangles and parallel lines.
Applications: The midpoint theorem is incredibly useful in various triangle-related problems, enabling efficient solutions and the derivation of additional properties.
Conclusion: The Significance of Midpoints in Geometry
The statement "X is the midpoint of WY and VZ" encapsulates a fundamental concept in geometry that has far-reaching implications. Understanding the properties of midpoints and their application within different geometric contexts is crucial for solving problems and grasping more advanced geometric concepts. This article has touched upon various aspects of midpoints, exploring scenarios, proving properties, and highlighting applications. By strengthening your understanding of midpoints, you gain a powerful tool to tackle a wide array of geometrical challenges. Further exploration of midpoint theorems and related concepts will unlock a deeper understanding of the elegant and interconnected nature of geometry. The seemingly simple idea of a midpoint forms the basis for far more complex and significant geometrical theorems and applications, underscoring its importance in the study of shapes and spaces.
Latest Posts
Latest Posts
-
What Unexpected Event Occurs After Frankenstein Passes Away
Jun 07, 2025
-
Match Each Element Of A Sonnet With The Correct Description
Jun 07, 2025
-
Which Expression Is A Prime Polynomial
Jun 07, 2025
-
Antonella Has Been Working With A Therapist
Jun 07, 2025
-
Which Of The Following Does Not Describe A Musical Motive
Jun 07, 2025
Related Post
Thank you for visiting our website which covers about X Is The Midpoint Of Wy And Vz . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.