Y 4x Rx 6 Solve For X
Breaking News Today
Jun 01, 2025 · 5 min read
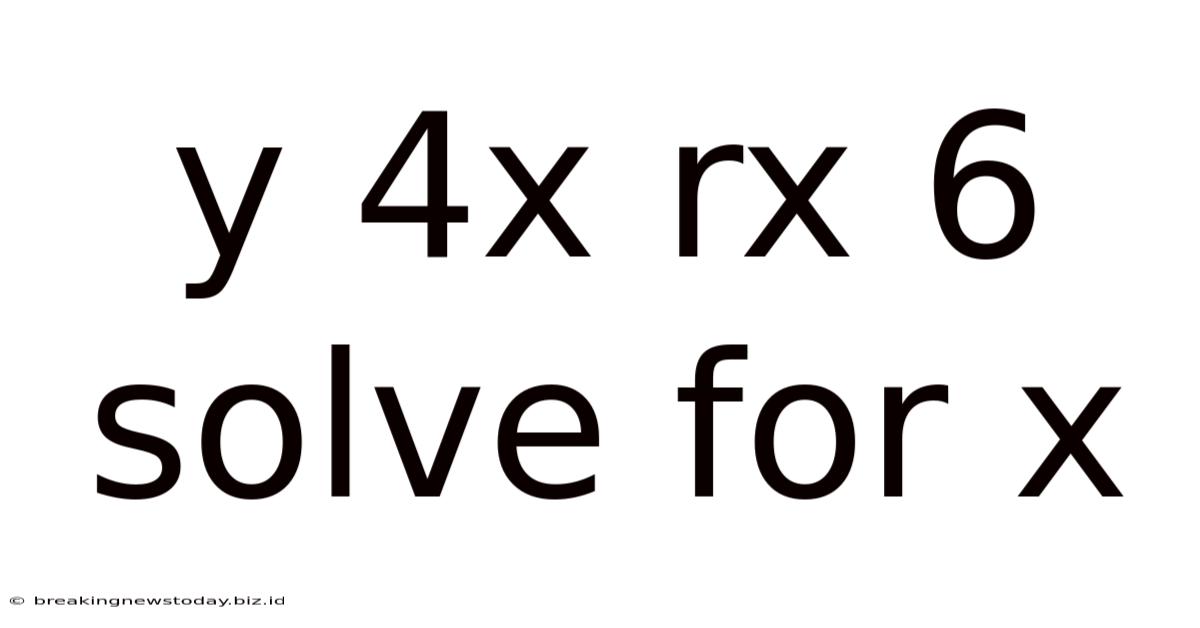
Table of Contents
Solving for x: A Comprehensive Guide to y = 4x + rx - 6
This article provides a detailed walkthrough of solving the equation y = 4x + rx - 6 for the variable x. We'll cover various approaches, from basic algebra to handling potential complexities, ensuring you gain a solid understanding of the process. We'll also discuss the importance of understanding the context of the equation and potential real-world applications.
Understanding the Equation: y = 4x + rx - 6
Before diving into the solution, let's analyze the equation itself. y = 4x + rx - 6 is a linear equation, meaning it represents a straight line when graphed. The presence of both 4x and rx indicates that the equation involves two terms containing the variable x, making the solution slightly more involved than simpler linear equations. The constant term, -6, represents the y-intercept – the point where the line crosses the y-axis.
The variable 'r' acts as a coefficient, implying that the solution for 'x' will likely depend on the value of 'r'. This makes it crucial to address potential scenarios involving 'r'.
Solving for x: Step-by-Step Approach
The goal is to isolate x on one side of the equation. Here’s a detailed step-by-step approach:
1. Combine like terms:
The equation contains two terms with x: 4x and rx. We can combine them by factoring out x:
y = x(4 + r) - 6
This simplification makes the next steps significantly easier.
2. Add 6 to both sides:
To isolate the term containing x, we need to move the constant term (-6) to the other side of the equation. We achieve this by adding 6 to both sides:
y + 6 = x(4 + r)
3. Consider the Value of (4 + r):
This is a crucial step. The next operation depends entirely on the value of (4 + r):
-
Case 1: (4 + r) ≠ 0: If the sum of 4 and r is not equal to zero, we can divide both sides of the equation by (4 + r) to isolate x:
x = (y + 6) / (4 + r)This is the general solution for
xwhenris any value other than -4. -
Case 2: (4 + r) = 0: If
(4 + r) = 0, which meansr = -4, the equation becomes:y + 6 = x(0)This simplifies to:
y + 6 = 0This means that
y = -6. In this specific case, there's no unique solution for x; any value of x will satisfy the equation when y = -6. The line represented by the equation becomes a horizontal line at y = -6.
Understanding the Solution and its Implications
The solution, x = (y + 6) / (4 + r), illustrates the relationship between x, y, and r. It's a formula that allows us to calculate the value of x given the values of y and r, provided that (4 + r) is not equal to zero.
Let’s consider a few examples to solidify understanding:
Example 1: If y = 10 and r = 2, then:
x = (10 + 6) / (4 + 2) = 16 / 6 = 8/3
Example 2: If y = 0 and r = -1, then:
x = (0 + 6) / (4 - 1) = 6 / 3 = 2
Example 3: If y = -6 and r = -4 (Case 2):
The equation becomes -6 + 6 = 0, which is always true, regardless of the value of x. Therefore, x can be any real number.
Practical Applications and Real-World Scenarios
Equations like y = 4x + rx - 6 are frequently encountered in various fields:
- Physics: They might represent relationships between variables such as velocity, time, and acceleration.
- Engineering: They can model various physical phenomena, particularly linear relationships between quantities.
- Economics: In economic modeling, such equations can represent relationships between price, quantity, and other economic variables.
- Finance: They might appear in calculations related to interest, investment growth, or debt management.
Understanding how to solve these equations is essential for analyzing and interpreting data in these and other disciplines.
Advanced Considerations: Handling Complexities
While we’ve covered the basic solution, let’s discuss potential complexities and how to address them:
- Non-linear extensions: If the equation were non-linear (e.g., containing terms like x², x³, etc.), the solution method would be different, often requiring more advanced techniques like the quadratic formula or other numerical methods.
- Systems of Equations: The equation might be part of a larger system of equations. Solving a system of equations would require using methods like substitution, elimination, or matrix operations.
- Constraints: There might be constraints on the values of x, y, or r. For instance, x might be limited to positive values only, or r might be constrained to a specific range. These constraints need to be considered when interpreting the solution.
- Dealing with Complex Numbers: In certain scenarios, depending on the values of y and r, the solution for x might involve complex numbers (numbers that include the imaginary unit 'i'). Understanding how to handle complex numbers becomes necessary.
Conclusion: Mastering the Solution
Solving the equation y = 4x + rx - 6 for x requires a systematic approach, encompassing understanding the equation's structure, combining like terms, considering the potential values of r, and correctly interpreting the results. The solution demonstrates a fundamental algebraic concept and serves as a building block for tackling more complex mathematical problems in various fields. Remembering to consider the special case where (4 + r) = 0 is crucial for a complete understanding of the solution space. By mastering this type of problem, you'll enhance your problem-solving skills and expand your understanding of linear equations and their applications. This knowledge is invaluable in numerous academic and professional settings. Further exploration into more complex algebraic concepts will build upon this foundation, enabling you to tackle even more challenging mathematical problems.
Latest Posts
Latest Posts
-
Complete The Coordinate Table For The Given Equation Xy 12
Jun 02, 2025
-
Which Sentence Best Revises Sentence 3 To Use Formal Language
Jun 02, 2025
-
Solve 9x Y 45 For Y
Jun 02, 2025
-
A An Is A Roughly Structured Outline Of Your Workout
Jun 02, 2025
-
Your Renpy Version Have Some Save Protection
Jun 02, 2025
Related Post
Thank you for visiting our website which covers about Y 4x Rx 6 Solve For X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.