1.12 Repeating As A Mixed Number
Breaking News Today
Jun 05, 2025 · 5 min read
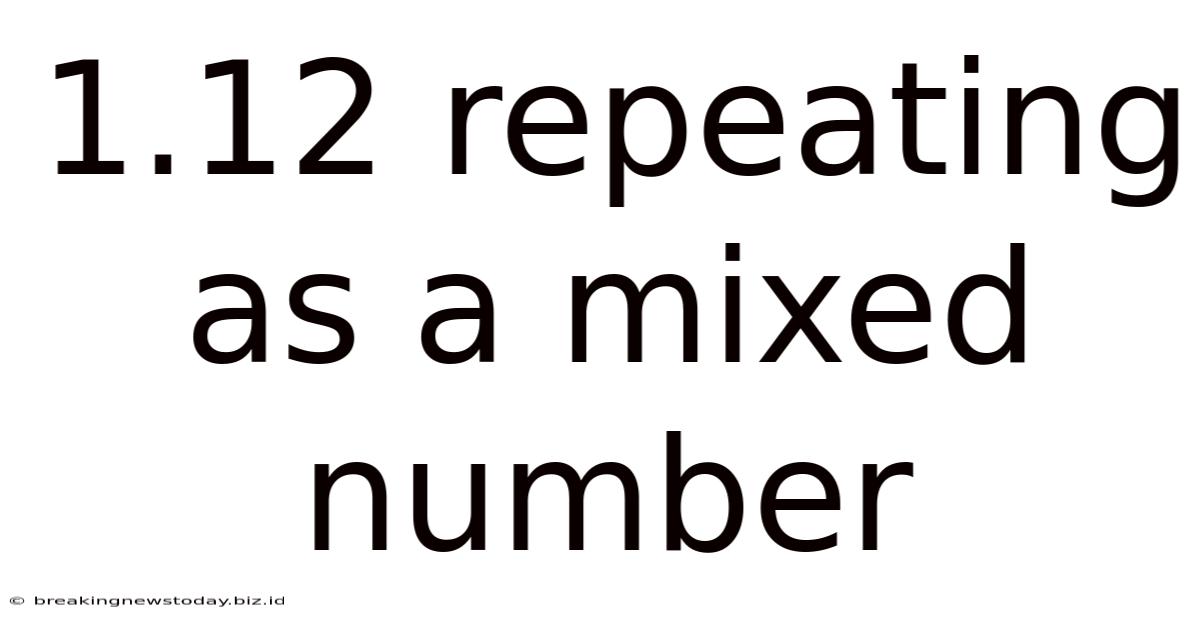
Table of Contents
1.12 Repeating as a Mixed Number: A Comprehensive Guide
The seemingly simple task of converting a repeating decimal like 1.121212... into a mixed number might appear daunting at first. However, with a structured approach and understanding of fundamental mathematical principles, the process becomes straightforward and even enjoyable. This comprehensive guide will walk you through the entire process, covering various methods and explaining the underlying concepts. We'll delve into the theory behind repeating decimals, explore different solution approaches, and offer practical examples to solidify your understanding.
Understanding Repeating Decimals and Mixed Numbers
Before we dive into the conversion process, let's solidify our understanding of the key terms involved:
Repeating Decimals: A repeating decimal, also known as a recurring decimal, is a decimal number that has a digit or a group of digits that repeat infinitely. The repeating part is often indicated by a bar placed over the repeating digits. For example, 1.121212... can be written as 1.¯¯12.
Mixed Numbers: A mixed number is a number that consists of a whole number and a proper fraction. For example, 1 ¾, 2 ⅔, and 5 ⅛ are all mixed numbers. They combine the simplicity of whole numbers with the precision of fractions.
Our goal is to transform the repeating decimal 1.¯¯12 into its equivalent mixed number representation. This involves expressing the repeating decimal as a fraction and then converting that fraction into a mixed number.
Method 1: Using Algebra to Solve for the Repeating Decimal
This method employs algebraic manipulation to solve for the value of the repeating decimal. It's a powerful technique applicable to various repeating decimals.
Step 1: Set up an Equation
Let's represent the repeating decimal, 1.¯¯12, with the variable 'x':
x = 1.¯¯12
Step 2: Multiply to Shift the Decimal
Multiply both sides of the equation by a power of 10 that shifts the repeating block to the left of the decimal point. In this case, we multiply by 100 because the repeating block has two digits:
100x = 112.¯¯12
Step 3: Subtract the Original Equation
Subtract the original equation (x = 1.¯¯12) from the equation obtained in Step 2:
100x - x = 112.¯¯12 - 1.¯¯12
This simplifies to:
99x = 111
Step 4: Solve for x
Solve for 'x' by dividing both sides by 99:
x = 111/99
Step 5: Simplify the Fraction
Simplify the fraction by finding the greatest common divisor (GCD) of the numerator and denominator. The GCD of 111 and 99 is 9. Dividing both the numerator and denominator by 9, we get:
x = 12/11
Step 6: Convert to a Mixed Number
Now, we convert the improper fraction 12/11 into a mixed number by performing division:
12 ÷ 11 = 1 with a remainder of 1
Therefore, the mixed number representation is:
x = 1 ⅛
So, 1.¯¯12 is equivalent to the mixed number 1 1/11.
Method 2: The Long Division Approach (Less Efficient for Repeating Decimals)
While less efficient than the algebraic method for repeating decimals, understanding long division offers a valuable alternative approach. This method is particularly useful for terminating decimals, but can become cumbersome with repeating decimals.
Step 1: Convert the Decimal to a Fraction
Treat the repeating decimal as a fraction. In our case, we could approximate 1.1212 to the fraction 11212/10000, but this would only be an approximation, not the exact value. The repeating nature makes this method less precise.
Step 2: Simplify the Fraction
If we used the approximate fraction above, we would need to simplify it by finding the GCD of the numerator and denominator. The resulting fraction is only an approximation of the true value.
Step 3: Convert the Fraction to a Mixed Number
This would involve long division. However, since the fraction obtained would be an approximation, the resulting mixed number would be an approximation as well. Therefore this method is not ideal for repeating decimals.
Why the Algebraic Method is Preferred for Repeating Decimals
The algebraic method is significantly superior to the long division method when dealing with repeating decimals because it directly addresses the repeating nature of the number. The long division method, when applied to approximations, fails to capture the precise value of the repeating decimal, leading to inaccuracies. The algebraic method, on the other hand, provides an exact representation.
Practical Applications and Further Exploration
Understanding the conversion of repeating decimals into mixed numbers is crucial in various fields, including:
- Engineering: Precise calculations in engineering often require converting decimal measurements to fractional equivalents for greater accuracy.
- Finance: Calculations involving interest rates or currency conversions may involve repeating decimals that need to be converted into simpler fractional forms.
- Computer Science: Representing numbers in different bases (binary, hexadecimal) often requires manipulation of decimal values, including repeating decimals.
- Mathematics: A strong understanding of decimal-fraction conversions forms the foundation for advanced mathematical concepts.
Troubleshooting Common Mistakes
-
Incorrect Multiplication: When shifting the decimal using multiplication by powers of 10, ensure that the multiplication is performed accurately. Errors at this step will propagate through the entire calculation.
-
Errors in Subtraction: Ensure the subtraction of the original equation from the multiplied equation is performed correctly. Mistakes in this step will affect the final result.
-
Improper Fraction Simplification: Finding the greatest common divisor is crucial for simplifying fractions to their lowest terms. Failure to do so results in a less concise representation of the mixed number.
Conclusion: Mastering Repeating Decimal Conversions
Converting the repeating decimal 1.¯¯12 to a mixed number underscores the importance of understanding fundamental mathematical principles and selecting appropriate methods. The algebraic method proves to be the most efficient and accurate approach when dealing with repeating decimals, providing an exact and concise representation. By mastering this technique, you'll enhance your mathematical proficiency and be equipped to handle similar conversions with confidence in various applications. Remember to practice and explore different scenarios to solidify your understanding. The key is to approach the problem methodically and double-check each step to ensure accuracy. The reward is a deeper grasp of number systems and their practical applications.
Latest Posts
Latest Posts
-
Which Are Vertical Angles Check All That Apply
Jun 06, 2025
-
The Student Made The Standard Curve Above
Jun 06, 2025
-
8 25 Of What Number Is 7 26
Jun 06, 2025
-
The Concave Of A Tape Measure Blade Is Designed To
Jun 06, 2025
-
What Design Principle Is Stressed For Experiments Or Observational Studies
Jun 06, 2025
Related Post
Thank you for visiting our website which covers about 1.12 Repeating As A Mixed Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.