1/2x - 2 0 On A Number Line
Breaking News Today
Jun 07, 2025 · 6 min read
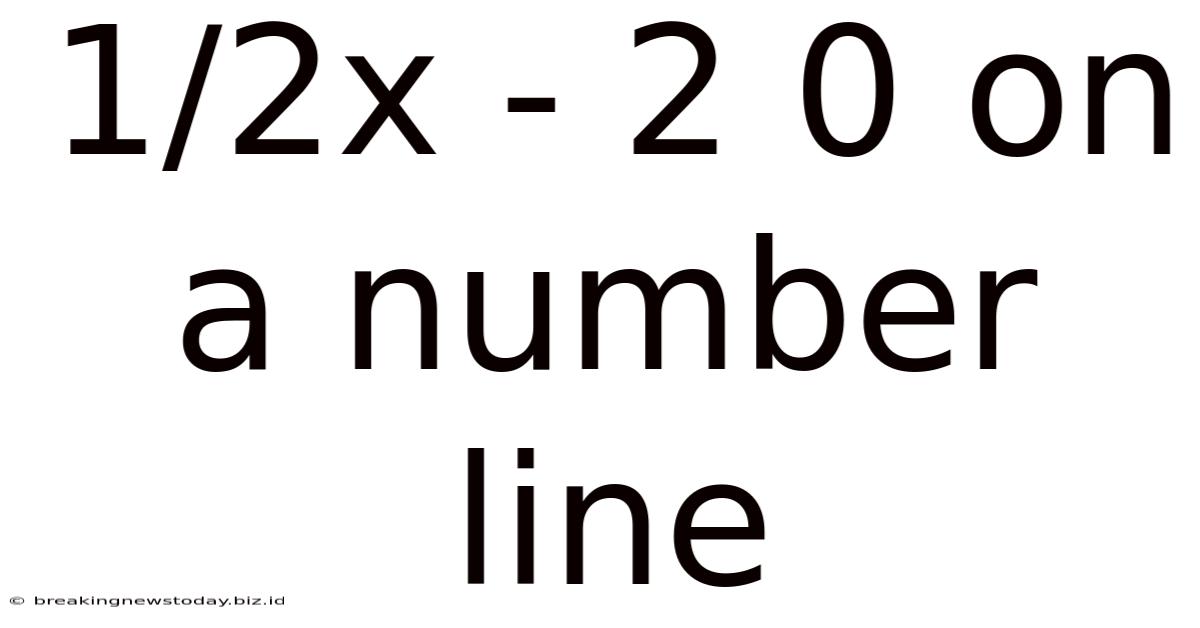
Table of Contents
Visualizing Inequalities: A Deep Dive into 1/2x - 2 > 0 on a Number Line
Understanding inequalities and representing them graphically on a number line is a fundamental skill in algebra. This article will provide a comprehensive guide on how to solve and represent the inequality 1/2x - 2 > 0 on a number line, explaining the steps involved and exploring the underlying concepts. We'll also delve into related topics to solidify your understanding.
Understanding the Inequality
The inequality 1/2x - 2 > 0 asks us to find all values of 'x' that make the expression 1/2x - 2 greater than zero. This means we're looking for the solution set where the expression results in a positive value. Let's break down the process of solving this inequality step-by-step.
Step 1: Isolating the Variable
Our first goal is to isolate the variable 'x' on one side of the inequality sign. We'll achieve this using inverse operations.
-
Add 2 to both sides: This eliminates the -2 on the left side. The inequality becomes: 1/2x > 2
-
Multiply both sides by 2: This gets rid of the fraction (1/2) multiplying 'x'. The inequality becomes: x > 4
This inequality, x > 4, tells us that all values of 'x' greater than 4 satisfy the original inequality 1/2x - 2 > 0.
Representing the Solution on a Number Line
A number line provides a visual representation of the solution set. Here's how to plot x > 4 on a number line:
-
Draw a number line: Draw a horizontal line with evenly spaced markings representing numbers.
-
Locate 4: Find the point representing the number 4 on the number line.
-
Mark the inequality: Since x is greater than 4 (not greater than or equal to), we use an open circle at 4. This signifies that 4 itself is not included in the solution set.
-
Shade the solution region: Shade the portion of the number line to the right of the open circle at 4. This shaded region represents all values of x that are greater than 4.
(Visual representation would be included here if this were a visual document. Imagine a number line with an open circle at 4 and the region to the right shaded.)
Interpreting the Solution
The shaded region on the number line visually demonstrates the solution set to the inequality 1/2x - 2 > 0. This means:
-
Any value greater than 4 satisfies the inequality. For example, x = 5, x = 10, and x = 100 all make the original expression 1/2x - 2 greater than 0.
-
4 itself does not satisfy the inequality. If you substitute x = 4 into the original expression, you get 1/2(4) - 2 = 0, which is not greater than 0.
Exploring Related Concepts
Let's expand our understanding by examining related scenarios and concepts:
1. Inequalities with "or equal to":
Consider the inequality 1/2x - 2 ≥ 0. The only difference is the inclusion of the "or equal to" symbol (≥). Solving this follows the same steps:
- 1/2x ≥ 2
- x ≥ 4
The graphical representation on the number line would now involve a closed circle at 4 (indicating that 4 is included in the solution set), with the region to the right shaded.
(Visual representation would be included here if this were a visual document. Imagine a number line with a closed circle at 4 and the region to the right shaded.)
2. Inequalities with "less than" or "less than or equal to":
Let's consider an inequality where the variable is less than a value. For example: -1/2x + 3 < 1
- Subtract 3 from both sides: -1/2x < -2
- Multiply both sides by -2. Important: When multiplying or dividing an inequality by a negative number, you must reverse the inequality sign. This gives us: x > 4
Notice that even though we started with "less than," the solution ended up being "greater than." The reversal of the inequality sign is crucial when dealing with negative multipliers or divisors. The graphical representation on the number line would be an open circle at 4 with the region to the right shaded.
(Visual representation would be included here if this were a visual document. Imagine a number line with an open circle at 4 and the region to the right shaded.)
3. Compound Inequalities:
Compound inequalities involve two inequality statements connected by "and" or "or". For example:
x > 2 and x < 6
This means x must be greater than 2 and less than 6 simultaneously. On the number line, this would be represented by an open circle at 2 and an open circle at 6, with the region between the two circles shaded.
(Visual representation would be included here if this were a visual document. Imagine a number line with open circles at 2 and 6, with the region between them shaded.)
x > 5 or x < 1
This means x is either greater than 5 or less than 1. On the number line, this would involve open circles at 1 and 5, with the regions to the left of 1 and to the right of 5 shaded.
(Visual representation would be included here if this were a visual document. Imagine a number line with open circles at 1 and 5, with the regions to the left of 1 and to the right of 5 shaded.)
4. Absolute Value Inequalities:
Absolute value inequalities introduce another layer of complexity. For example:
|x - 3| < 2
This inequality means the distance between x and 3 is less than 2. To solve this, we consider two separate inequalities:
x - 3 < 2 and -(x - 3) < 2
Solving these gives us:
x < 5 and x > 1
This is equivalent to 1 < x < 5. The graphical representation would show open circles at 1 and 5, with the region between them shaded.
(Visual representation would be included here if this were a visual document. Imagine a number line with open circles at 1 and 5, with the region between them shaded.)
Practical Applications
Understanding inequalities and their graphical representations has numerous practical applications in various fields:
-
Engineering: Determining allowable tolerances in manufacturing processes.
-
Finance: Modeling financial growth or decline.
-
Physics: Describing the range of possible values for physical quantities.
-
Computer Science: Setting constraints in algorithms and data structures.
-
Statistics: Defining confidence intervals and determining statistical significance.
Conclusion
Solving and representing inequalities on a number line is a crucial skill in algebra and has wide-ranging applications. By mastering the techniques outlined in this article, you'll develop a solid foundation for more advanced mathematical concepts. Remember to carefully consider the inequality symbols, pay attention to the rules for manipulating inequalities (especially when multiplying or dividing by negative numbers), and always visualize your solution on a number line for a clearer understanding. Practice solving a variety of inequality problems to reinforce your understanding and build confidence in tackling more complex mathematical challenges.
Latest Posts
Latest Posts
-
Which Of The Following Is A Do Regarding Scannable R Sum S
Jun 07, 2025
-
Which Expression Is Equivalent To Sin 7pi 6
Jun 07, 2025
-
Tomatoes Represent A Small Subset Of Food So Tomatoes Are
Jun 07, 2025
-
A Family Has Two Cats Named Gordo And Flaco
Jun 07, 2025
-
Break Apart The Second Addend To Find 56 38
Jun 07, 2025
Related Post
Thank you for visiting our website which covers about 1/2x - 2 0 On A Number Line . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.