15 32 5 13 82 7 1
Breaking News Today
Jun 08, 2025 · 4 min read
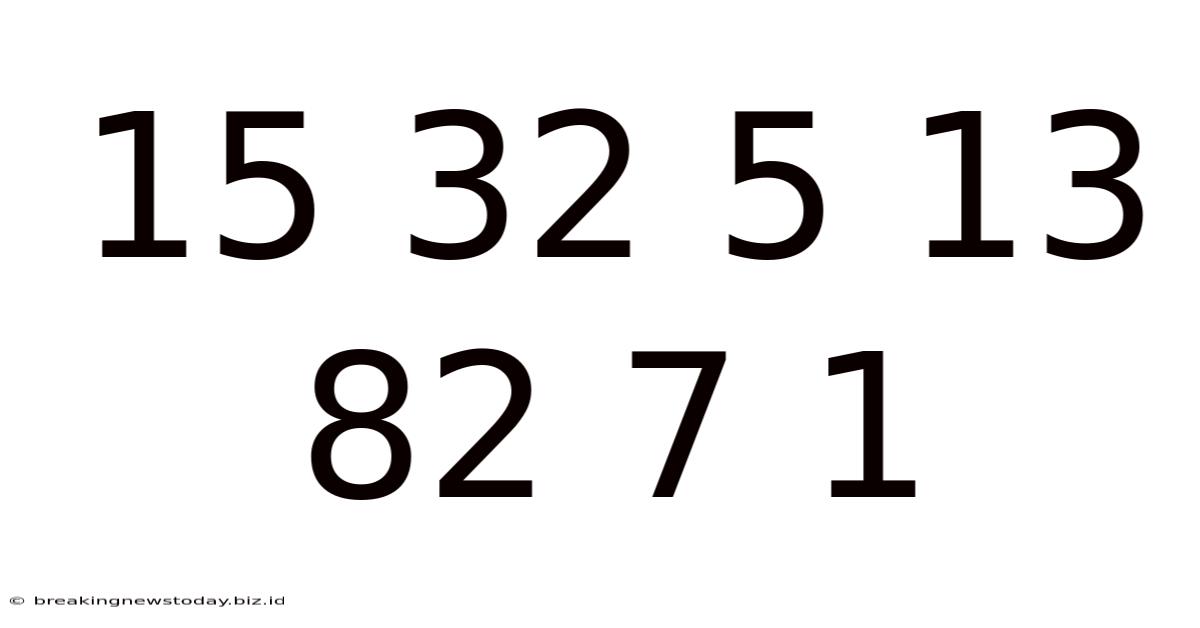
Table of Contents
Unraveling the Enigma: Exploring the Sequence 15 32 5 13 82 7 1
The seemingly random sequence 15, 32, 5, 13, 82, 7, 1 presents a fascinating puzzle. At first glance, it appears chaotic, devoid of any discernible pattern. However, with careful analysis and the application of various mathematical and logical approaches, we can begin to uncover potential underlying structures and explore possible interpretations. This article delves deep into this numerical sequence, examining various possibilities and offering potential explanations for its apparent randomness.
Initial Observations and Approaches
Before delving into complex mathematical models, let's start with some basic observations:
-
Magnitude Variation: The numbers vary greatly in magnitude, ranging from a single digit (1, 5, 7) to a two-digit number (13, 15, 32) and even a three-digit number (82). This wide range immediately suggests that a simple arithmetic progression or geometric progression is unlikely.
-
Prime Numbers: The sequence contains some prime numbers (5, 7, 13), but their distribution isn't regular, hinting that primality isn't the primary defining characteristic.
-
Lack of Obvious Arithmetic Relationships: Simple arithmetic operations (addition, subtraction, multiplication, division) between consecutive numbers don't reveal any consistent pattern.
-
Potential for Hidden Patterns: The apparent randomness might mask a more subtle pattern, requiring a more sophisticated approach to unveil.
Exploring Potential Patterns: Mathematical Perspectives
Given the lack of readily apparent patterns, let's consider some more intricate mathematical approaches:
1. Fibonacci-like Sequences and Variations
Fibonacci sequences are known for their elegant patterns. While this sequence doesn't directly follow a Fibonacci sequence (where each number is the sum of the two preceding ones), we might explore variations. We could look for:
-
Generalized Fibonacci Sequences: These sequences allow for different starting values and may involve other arithmetic operations besides simple addition.
-
Modified Fibonacci Sequences: Perhaps the sequence is a transformation or encoding of a Fibonacci-like sequence.
2. Modular Arithmetic and Residue Classes
Modular arithmetic might reveal hidden relationships. For example, we could examine the remainders when each number is divided by a specific modulus (e.g., 2, 3, 5, etc.). Consistent patterns in the remainders could indicate a hidden structure.
3. Polynomial Functions and Curve Fitting
It's possible the sequence is generated by a polynomial function. If we assign each number a position (1st, 2nd, 3rd, etc.), we could attempt to fit a polynomial curve to the data points. This requires advanced mathematical techniques and tools like regression analysis. However, the limited number of data points makes it challenging to accurately determine a high-order polynomial.
4. Number Theory Approaches
Number theory provides a powerful framework for understanding number sequences. Concepts like:
-
Divisibility: Analyzing the divisors of each number might reveal common factors or patterns.
-
Congruences: Exploring congruences between numbers modulo different integers could uncover hidden relationships.
-
Prime Factorization: The prime factorization of each number might reveal unexpected connections.
could be used to explore deeper relationships within the sequence.
Beyond Mathematics: Exploring Alternative Interpretations
The sequence's apparent randomness could suggest interpretations beyond purely mathematical ones:
1. Cryptography and Encoding
The sequence could represent a simple cipher or code. A key or algorithm might be needed to decipher its true meaning. The context in which this sequence was found (e.g., a message, a game, a computer program) would be essential for deciphering it.
2. Random Number Generation
The numbers could be a sequence generated by a pseudo-random number generator (PRNG). Analyzing the properties of the sequence (e.g., its distribution, autocorrelation) might help identify the algorithm used to generate it. However, without knowing the specific PRNG used, this remains highly speculative.
3. Physical or Natural Phenomena
In some cases, seemingly random sequences might represent data from a physical process or natural phenomenon. However, the sequence's lack of context makes this interpretation highly improbable without additional information.
The Limitations of Analysis
It's crucial to acknowledge the limitations of analyzing a short sequence like this:
-
Insufficient Data: A longer sequence would provide more evidence and make it easier to identify underlying patterns.
-
Multiple Explanations: Several different explanations could potentially fit the data. A longer sequence or additional context would be necessary to differentiate between them.
-
Computational Complexity: For complex mathematical models (like polynomial fitting or exploring sophisticated number theory concepts), significant computational power might be necessary.
Conclusion: The Ongoing Search for Meaning
The sequence 15 32 5 13 82 7 1 remains an enigma. While various mathematical and logical approaches have been explored, none provide a definitive, universally accepted solution. The lack of context surrounding the sequence greatly hinders any conclusive interpretation. Its apparent randomness challenges our assumptions about patterns and order in numerical data. The quest to unravel its mystery serves as a reminder of the complexity and beauty inherent in mathematical sequences, highlighting the need for more data, contextual information, and further investigation to reach a satisfying conclusion. This exploration, however, highlights the power of applying multiple perspectives to decipher seemingly chaotic data. Further research, potentially including the use of advanced statistical methods and machine learning techniques, might uncover hidden patterns or relationships in this seemingly random sequence. The challenge remains open, inviting further exploration and investigation. Perhaps, with more information or a longer sequence, the underlying pattern will finally reveal itself.
Latest Posts
Latest Posts
-
Which Is Equivalent To 80 1 4x
Jun 08, 2025
-
How Could Caravans Passing Through Babylon Be Helped By Astronomers
Jun 08, 2025
-
How Many One Degree Angles Does An 80 Degree Angle Turn Through
Jun 08, 2025
-
Which Expression Is Equivalent To Mc009 1 Jpg
Jun 08, 2025
-
You Have Been Sick With Diarrhea What Answer
Jun 08, 2025
Related Post
Thank you for visiting our website which covers about 15 32 5 13 82 7 1 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.