16 3 9 10 2 5
Breaking News Today
Jun 08, 2025 · 5 min read
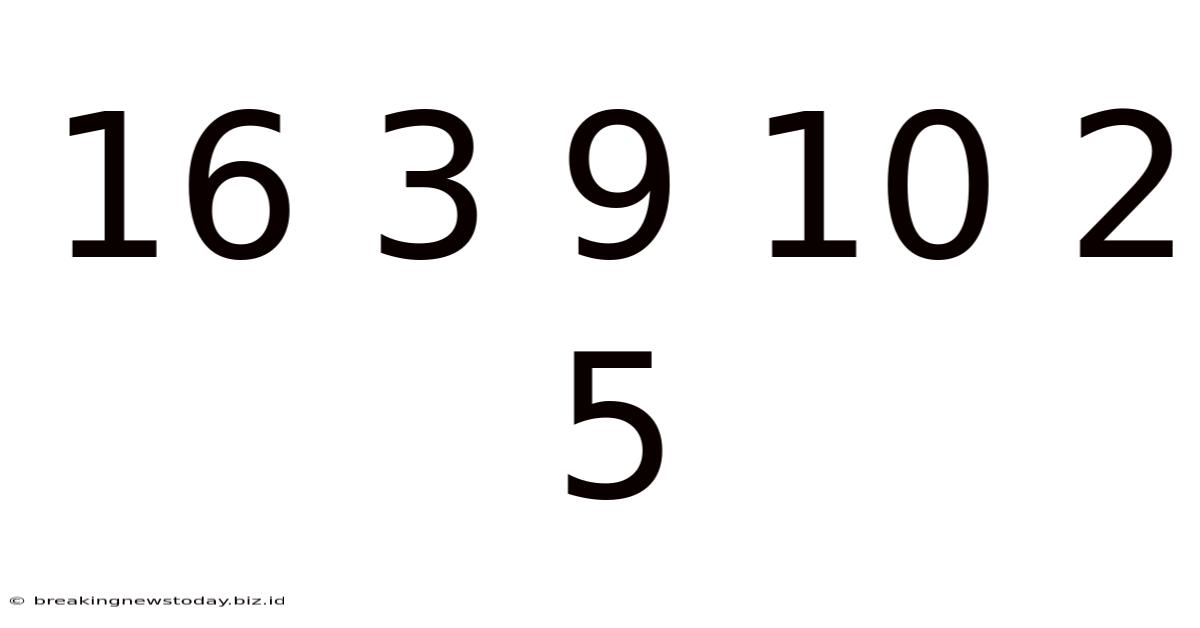
Table of Contents
Decoding the Sequence: 16 3 9 10 2 5 – A Deep Dive into Number Patterns and Problem-Solving
The seemingly innocuous sequence "16 3 9 10 2 5" holds within it a fascinating challenge. At first glance, it appears random. However, a closer inspection reveals the potential for multiple interpretations and solutions, highlighting the power of pattern recognition, logical reasoning, and creative problem-solving. This article delves into various approaches to understanding this numerical sequence, exploring different mathematical and logical perspectives, and ultimately demonstrating the richness inherent in seemingly simple problems.
The Allure of Number Sequences
Number sequences have captivated mathematicians and puzzle enthusiasts for centuries. Their appeal lies in the challenge they present: to decipher the underlying rule or pattern that governs their progression. Solving these sequences isn't merely about finding an answer; it's about honing critical thinking skills, developing analytical abilities, and fostering creative problem-solving strategies. This particular sequence, "16 3 9 10 2 5," provides an excellent case study in this regard. Its apparent randomness invites multiple interpretations, showcasing the diverse approaches that can be applied.
Potential Interpretations and Solutions
Let's explore some potential interpretations and solutions for the sequence 16 3 9 10 2 5. The absence of an immediately obvious pattern necessitates a more systematic approach:
1. Searching for Arithmetic Relationships
One of the first approaches is to look for arithmetic relationships between consecutive numbers. However, simple addition, subtraction, multiplication, or division doesn't reveal a consistent pattern within this sequence. The differences between consecutive numbers are irregular and don't suggest a straightforward arithmetic progression.
- 16 - 3 = 13
- 3 - 9 = -6
- 9 - 10 = -1
- 10 - 2 = 8
- 2 - 5 = -3
2. Exploring Geometric Progressions
Similarly, examining for geometric progressions (where each number is obtained by multiplying the previous number by a constant) doesn't yield a consistent pattern. The ratios between consecutive numbers are varied and lack a unifying factor.
3. Considering Alternative Mathematical Operations
We can broaden our search to incorporate more complex mathematical operations. Could there be a relationship based on prime factorization, modular arithmetic, or other mathematical concepts? This requires a deeper investigation, possibly involving computer programming to test various combinations of operations.
4. The Significance of the Numbers Themselves
Another approach is to analyze the intrinsic properties of the individual numbers. Are they prime numbers, perfect squares, Fibonacci numbers, or do they hold significance within specific mathematical contexts? This line of inquiry allows for the exploration of number theory and its applications in pattern recognition. While none of the numbers are immediately identifiable as belonging to a specific known number sequence, this doesn't rule out more complex relationships.
5. Analyzing the Sequence in Groups
Instead of examining consecutive numbers, we can try analyzing the sequence in smaller groups. Could there be a pattern within the first three numbers, then the next two, and finally the last one? This approach allows for flexibility in pattern detection. For example:
- 16, 3, 9: These numbers might relate to powers of 3 (3², 3¹, 3⁰ which equals 1). There is a missing 1 to form a clear pattern here, suggesting it's possible but not definite.
6. External Contextual Clues
It's also important to consider whether there is any external context to this number sequence. Was it found in a specific book, a code, or a puzzle? The origin of the sequence might provide valuable clues that help decipher its hidden rules. Without this context, we're limited to purely mathematical analyses.
The Importance of Problem-Solving Strategies
The exploration of this numerical sequence demonstrates the importance of adopting various problem-solving strategies. A methodical approach, combining both intuition and rigorous analysis, is often necessary to unravel complex patterns. This includes:
- Trial and Error: Testing various hypotheses and discarding those that don't fit.
- Pattern Recognition: Identifying recurring elements or relationships within the data.
- Logical Reasoning: Using deductive and inductive reasoning to draw conclusions.
- Lateral Thinking: Considering unconventional approaches and perspectives.
- Collaboration: Discussing the problem with others to gain different viewpoints.
Expanding the Scope of the Problem
The ambiguity of the sequence invites us to consider broader questions. What if the sequence is incomplete? What if it's a fragment of a larger, more complex pattern? These possibilities open up avenues for further exploration and demonstrate the importance of considering context and the limitations of the available data.
Conclusion: The Open-Ended Nature of Pattern Recognition
The sequence "16 3 9 10 2 5" serves as a compelling example of the open-ended nature of pattern recognition. While we may not arrive at a single, definitive solution without additional context, the process of exploring different approaches strengthens our analytical and problem-solving skills. The ambiguity of the sequence underscores the creativity and flexibility required in deciphering seemingly random patterns. It highlights the fact that mathematical puzzles often have multiple solutions, and the journey of exploration is as valuable as the final answer. The experience of grappling with this sequence enhances our capacity to tackle similar challenges in various fields, from cryptography to data science and beyond.
The beauty of number sequences, like this one, lies in their ability to stimulate our minds, encouraging us to think critically, creatively, and methodically. This process of exploration is a testament to the inherent fascination and intellectual rewards of unraveling mathematical puzzles. Ultimately, the journey of deciphering this seemingly simple sequence is a journey of discovery, highlighting the power of human ingenuity and the enduring allure of numbers.
Latest Posts
Latest Posts
-
Which Statement Best Describes The Function Shown In The Graph
Jun 08, 2025
-
0 6 Divided By 10 To The Power Of 2
Jun 08, 2025
-
Use The Equation Es001 1 Jpg How Many Potential Solutions Are There
Jun 08, 2025
-
All Of The Following Are Strengths Of Payback Except
Jun 08, 2025
-
Dajuan Has A Family In Jamaica
Jun 08, 2025
Related Post
Thank you for visiting our website which covers about 16 3 9 10 2 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.