3 4 Z 2 5 2z
Breaking News Today
Jun 07, 2025 · 5 min read
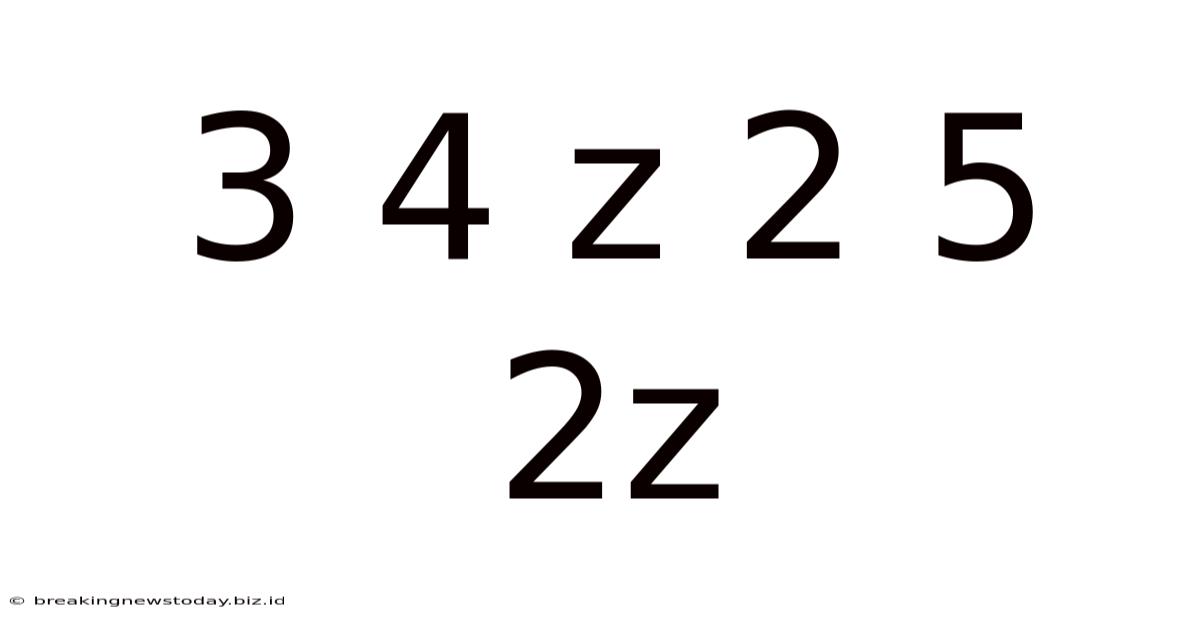
Table of Contents
Decoding the Enigma: A Deep Dive into the Sequence "3 4 z 2 5 2z"
The seemingly random sequence "3 4 z 2 5 2z" presents a fascinating puzzle. Without context, deciphering its meaning is challenging, yet the very ambiguity invites exploration and sparks creativity. This article will delve into various potential interpretations, exploring mathematical, linguistic, and even cryptographic possibilities, ultimately highlighting the power of pattern recognition and analytical thinking in deciphering cryptic information.
The Mathematical Perspective: Number Patterns and Sequences
Let's start by focusing on the numerical components: 3, 4, 2, 5, 2. Immediately, we see a lack of consistent mathematical progression. It's not an arithmetic sequence (constant difference) nor a geometric sequence (constant ratio). However, we can explore other possibilities:
Fibonacci-like Sequences and Variations
While not a strict Fibonacci sequence (where each number is the sum of the two preceding ones), we might consider variations. Could it be a sequence where differences between consecutive numbers form a pattern? Or perhaps a sequence modulo a certain number? Investigating these avenues might reveal hidden mathematical structure. For instance, we can examine the differences:
- 4 - 3 = 1
- 2 - 4 = -2
- 5 - 2 = 3
- 2 - 5 = -3
This doesn't immediately reveal a clear pattern, but it’s a starting point for further analysis. We could also explore modular arithmetic; perhaps the numbers represent remainders after division by a specific integer. This line of inquiry requires extensive testing with different moduli to find a potential underlying mathematical pattern.
Prime Numbers and Factorization
The numbers themselves could be significant based on their prime factorization. The prime factorization of each number is:
- 2: 2
- 3: 3
- 4: 2 x 2
- 5: 5
No immediately obvious pattern emerges from these prime factorizations, but the frequency of the number 2 might hold significance. Perhaps the sequence is related to a more complex mathematical concept involving prime numbers and their properties. Further investigation could involve exploring connections to concepts like prime gaps, twin primes, or other prime-related sequences.
The Linguistic and Cryptographic Angle: Letters and Codes
The inclusion of the letter "z" introduces a linguistic and possibly cryptographic dimension to the sequence. This suggests a potential code or cipher.
Simple Substitution Ciphers
A straightforward approach is to consider a simple substitution cipher, where each number corresponds to a letter of the alphabet. For example, "3" could represent "C", "4" could represent "D," and so on. However, this leads to inconsistencies with the inclusion of "z." A simple A=1, B=2... Z=26 mapping doesn't directly translate the sequence into a meaningful word or phrase.
More Complex Ciphers
More advanced ciphers are possible. We could be dealing with:
- Polyalphabetic Substitution: Different substitutions are used for each number in the sequence.
- Affine Cipher: This involves a linear transformation applied to each number.
- Vigenère Cipher: This uses a keyword to encrypt the sequence.
To break these ciphers, we would need additional information or context. The presence of repeated "2" and "z" might provide clues. Frequency analysis, a common technique used in cryptanalysis, could help identify potential patterns within the cipher.
Letter Placement and Significance
The position of the "z" within the numerical sequence might hold significance. It could represent a delimiter, a break, or a signal to switch encryption methods. Alternatively, the "z" could be acting as a numerical value itself, maybe representing the end of an alphabet, or perhaps it has a specific value assigned within a larger code system. The relative position of "z" could be part of the hidden code.
Context is Key: The Importance of External Information
Without additional information about the origin or context of this sequence, our analysis remains speculative. To effectively decode "3 4 z 2 5 2z," we need more context. Consider these scenarios:
- A Code within a Larger System: The sequence could be part of a larger system or message, and understanding this system is crucial for interpretation.
- A Specific System or Application: This sequence might be related to a specific application, such as computer programming, a game, or a particular protocol. Knowing the context can illuminate the meaning.
- Coordinates or Markers: In navigation or mapping, such sequences could represent coordinates or markers within a specific system.
- Musical Notation: Numerical sequences can sometimes represent musical notes or rhythms.
Expanding the Analysis: Pattern Recognition and Analytical Skills
The process of trying to decode "3 4 z 2 5 2z" underscores the importance of pattern recognition and analytical thinking. These are essential skills applicable to diverse fields, including:
- Data Analysis: The process of finding patterns in datasets mirrors our attempt to decipher the sequence.
- Code Breaking: The cryptographic considerations are directly related to code breaking techniques.
- Problem Solving: The entire exercise reflects the core aspects of problem-solving – analyzing the given data, formulating hypotheses, and testing different solutions.
- Critical Thinking: Formulating different interpretations and evaluating their plausibility are central to critical thinking.
Conclusion: The Ongoing Mystery and the Power of Inquiry
The sequence "3 4 z 2 5 2z" remains an enigma without further context. However, our exploration highlights the versatility of analytical thinking and the various approaches that can be applied to decipher cryptic information. Mathematical analysis, linguistic interpretation, and consideration of cryptographic techniques reveal the complexity and potential richness hidden within even seemingly simple sequences. The lack of immediate clarity should not be discouraging; rather, it emphasizes the value of persistent inquiry and methodical investigation when facing complex puzzles. The process of attempting to solve such puzzles develops crucial problem-solving skills with wide-ranging applications. Ultimately, the quest to decipher "3 4 z 2 5 2z" is a testament to the power of human curiosity and the rewarding journey of unraveling the unknown. The mystery remains, but the exploration itself is insightful and valuable.
Latest Posts
Latest Posts
-
How Many Tenths Are In 3 10
Jun 07, 2025
-
Four Times A Number Divided By 8 Is 3
Jun 07, 2025
-
7696 Divided By 52 With Remainder
Jun 07, 2025
-
According To Section Ii Of Dd Form 626
Jun 07, 2025
-
The National Security Advisor Supervises The Staff Of The
Jun 07, 2025
Related Post
Thank you for visiting our website which covers about 3 4 Z 2 5 2z . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.