4x 5 7 4y Solve For Y
Breaking News Today
Jun 02, 2025 · 4 min read
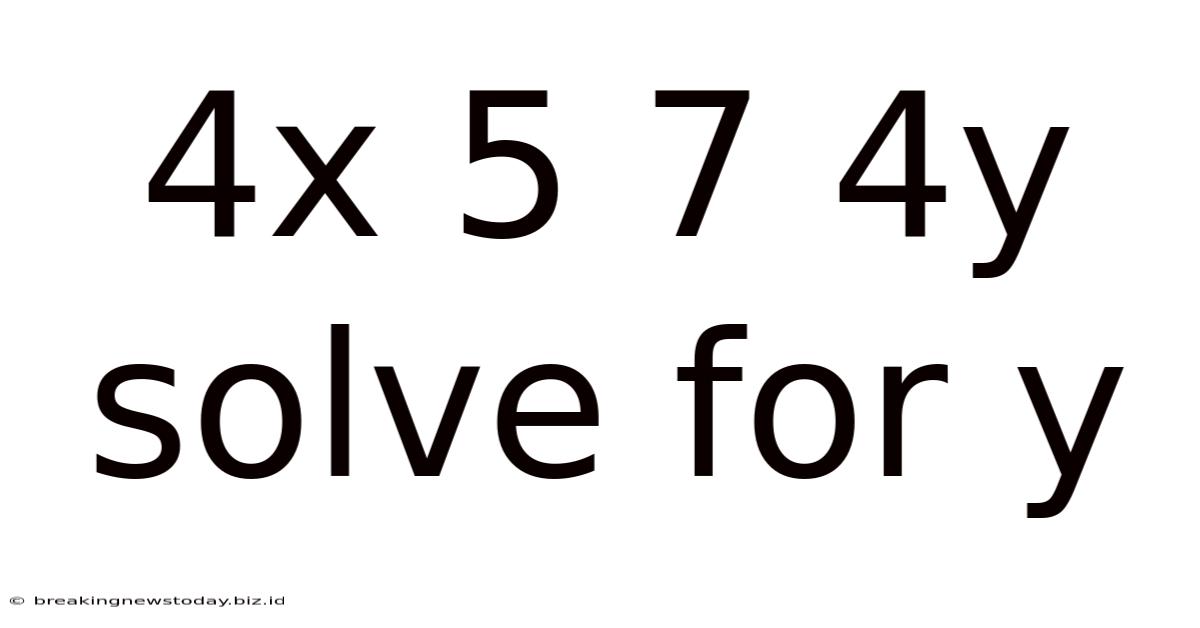
Table of Contents
Solving for 'y': A Deep Dive into the Equation 4x + 5 = 7 + 4y
This article provides a comprehensive guide on how to solve the algebraic equation 4x + 5 = 7 + 4y for 'y'. We'll explore the fundamental principles of algebra involved, demonstrate the step-by-step solution process, and discuss various approaches to tackling similar equations. Furthermore, we'll touch upon the importance of understanding the underlying concepts and how this skill translates to more complex mathematical problems.
Understanding the Equation: 4x + 5 = 7 + 4y
Before we delve into the solution, let's break down the equation: 4x + 5 = 7 + 4y. This is a linear equation with two variables, 'x' and 'y'. The goal is to isolate 'y' on one side of the equation, expressing it in terms of 'x'. This means we want to manipulate the equation so that it's in the form y = ... where the right-hand side contains only 'x' and constants.
Key Algebraic Concepts
Several core algebraic principles will guide our solution:
- Equality: The fundamental principle of equality states that whatever operation you perform on one side of an equation, you must perform the same operation on the other side to maintain balance.
- Inverse Operations: To isolate a variable, we utilize inverse operations. Addition and subtraction are inverse operations, as are multiplication and division.
- Combining Like Terms: This involves simplifying the equation by grouping terms containing the same variable together.
Solving for 'y': A Step-by-Step Approach
Now, let's proceed with solving the equation for 'y':
1. Isolate the term with 'y':
Our initial equation is: 4x + 5 = 7 + 4y
To isolate the term with 'y' (which is 4y), we need to subtract 7 from both sides of the equation:
4x + 5 - 7 = 7 + 4y - 7
This simplifies to:
4x - 2 = 4y
2. Solve for 'y':
Now, we have 4x - 2 = 4y. To isolate 'y', we divide both sides of the equation by 4:
(4x - 2) / 4 = (4y) / 4
This simplifies to:
x - 1/2 = y
or, more conventionally written:
y = x - 1/2
Therefore, we have successfully solved for 'y' in terms of 'x'. The solution is y = x - 1/2.
Verification: Checking Your Solution
It's crucial to verify your solution to ensure accuracy. We can do this by substituting a value for 'x' into both the original equation and our solved equation for 'y', and checking if they yield the same result.
Let's choose x = 2 as an example:
Original Equation:
4x + 5 = 7 + 4y
4(2) + 5 = 7 + 4y
8 + 5 = 7 + 4y
13 = 7 + 4y
13 - 7 = 4y
6 = 4y
y = 6/4 = 3/2 = 1.5
Solved Equation:
y = x - 1/2
y = 2 - 1/2
y = 3/2 = 1.5
Both equations yield the same value for 'y' (1.5) when x = 2. This verifies the accuracy of our solution: y = x - 1/2.
Alternative Approaches and Considerations
While the above method is straightforward, let's explore alternative approaches and considerations:
1. Subtracting the 'x' term first:
We could have started by subtracting 4x from both sides of the original equation:
4x + 5 - 4x = 7 + 4y - 4x
5 = 7 + 4y - 4x
Then subtract 7 from both sides:
5 - 7 = 4y - 4x
-2 = 4y - 4x
Divide by 4:
-1/2 = y - x
Rearrange:
y = x - 1/2
This yields the same result, demonstrating that the order of operations can sometimes be adjusted strategically.
2. Dealing with Fractions:
If the equation involved fractions, we would first find a common denominator to simplify the equation before proceeding with the steps outlined above.
3. Applications in Real-World Scenarios:
Linear equations like this appear frequently in various real-world contexts, including:
- Physics: Modeling relationships between variables like velocity, time, and distance.
- Economics: Analyzing supply and demand curves.
- Engineering: Solving for unknown quantities in design calculations.
Expanding Your Understanding: Further Exploration
Mastering the solution of linear equations forms a crucial foundation for tackling more complex algebraic problems. Here are some areas you can explore to expand your understanding:
- Systems of Equations: These involve solving for multiple variables in multiple equations simultaneously. Techniques like substitution and elimination are commonly employed.
- Quadratic Equations: These involve equations with squared variables (e.g., x²). Solution methods include factoring, the quadratic formula, and completing the square.
- Inequalities: These involve equations using inequality symbols (<, >, ≤, ≥). The solution process often involves similar algebraic manipulation but with careful consideration of the inequality signs.
Conclusion: Mastering Algebraic Skills
Solving the equation 4x + 5 = 7 + 4y for 'y' is a fundamental exercise in algebra. By understanding the underlying principles of equality, inverse operations, and combining like terms, and practicing various solution approaches, you can build a strong foundation for tackling more advanced mathematical concepts. Remember to always verify your solutions, and explore more complex equations to further solidify your understanding. The ability to confidently manipulate equations is a valuable skill with applications in numerous fields. Continue practicing and expanding your knowledge, and you’ll find that even the most complex equations become progressively easier to solve.
Latest Posts
Latest Posts
-
The Following Excerpt Features A Musical Ensemble
Jun 04, 2025
-
Identify The Vertex Of The Function Graphed Below
Jun 04, 2025
-
Which Quotation Correctly Uses Ellipsis To Shorten Twains Words
Jun 04, 2025
-
Completely Factor The Expression 18x2 78x 60
Jun 04, 2025
-
Choose The Correct Solution And Graph For The Inequality
Jun 04, 2025
Related Post
Thank you for visiting our website which covers about 4x 5 7 4y Solve For Y . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.