6 Is Subtracted From The Square Of A Number.
Breaking News Today
Jun 05, 2025 · 5 min read
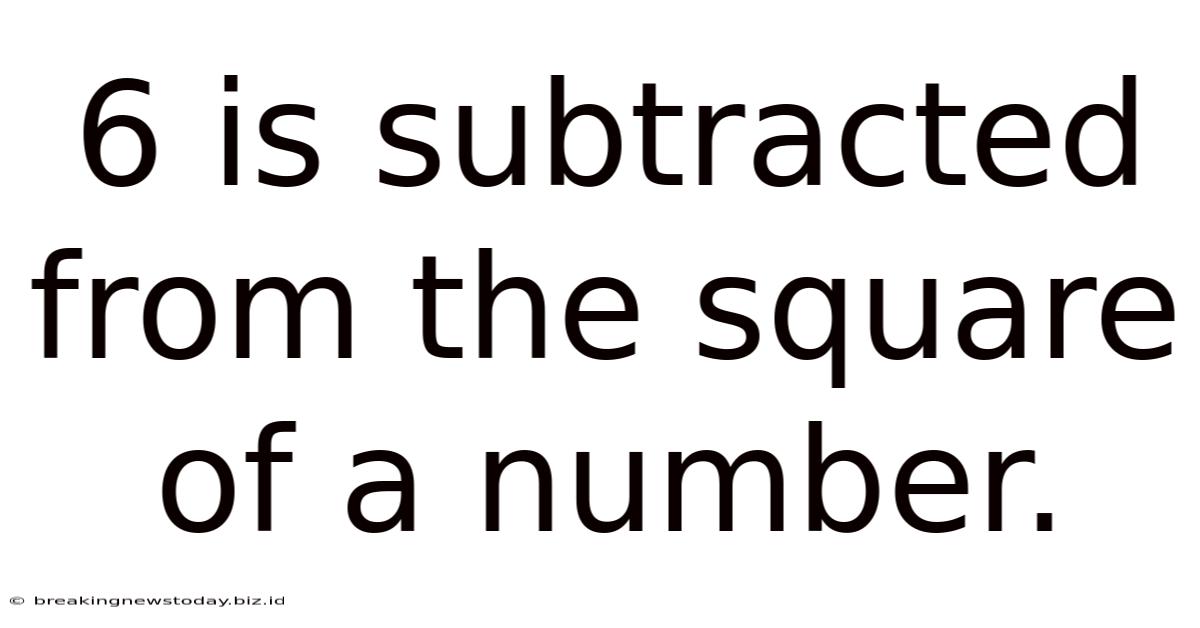
Table of Contents
6 is Subtracted from the Square of a Number: A Deep Dive into Mathematical Exploration
This seemingly simple phrase, "6 is subtracted from the square of a number," opens the door to a fascinating exploration of algebra, number theory, and even problem-solving strategies. This article will delve into this concept, examining its various interpretations, applications, and the rich mathematical landscape it unveils.
Understanding the Core Concept
The phrase itself translates directly into an algebraic expression: x² - 6, where 'x' represents the unknown number. This expression forms the foundation for numerous mathematical investigations. We can analyze it in several ways, each revealing different aspects of its nature.
1. Finding the Value of x
The most straightforward approach involves solving for 'x' given a specific result. For example, if the expression x² - 6 equals 10, we can set up an equation:
x² - 6 = 10
Solving this equation involves basic algebraic manipulation:
- Add 6 to both sides: x² = 16
- Take the square root of both sides: x = ±4
This demonstrates that there can be multiple solutions (in this case, 4 and -4) depending on the context of the problem. The sign (+ or -) matters significantly, especially when dealing with real-world applications where negative solutions might not be applicable.
2. Exploring the Graph of x² - 6
Visualizing the expression as a function, f(x) = x² - 6, provides further insights. This is a parabola, a U-shaped curve, shifted six units downwards from the standard parabola, f(x) = x².
-
Vertex: The vertex of the parabola represents the minimum value of the function. In this case, the vertex is at (0, -6). This means the smallest possible result of subtracting 6 from the square of a number is -6, occurring when x = 0.
-
Roots/Zeros: The roots, or zeros, of the function are the x-values where f(x) = 0. To find these, we solve the equation x² - 6 = 0:
x² = 6 x = ±√6
These are the points where the parabola intersects the x-axis. They are irrational numbers, approximately ±2.45.
-
Symmetry: Parabolas are symmetrical around their vertex. This means that for every x-value, there's a corresponding -x-value that produces the same y-value (except for the vertex itself).
By graphing this function, we can quickly visualize the behavior of the expression for various values of x. This visual representation is crucial for understanding its properties.
Applications and Real-World Examples
The expression x² - 6, while seemingly abstract, finds application in various real-world scenarios:
1. Area Calculations
Imagine a square with sides of length (x + √6) and (x - √6). Its area would be calculated as:
(x + √6)(x - √6) = x² - 6
This illustrates how the expression can represent the area of a specific geometric shape. By manipulating the lengths, we can find areas based on different values of x.
2. Physics and Projectile Motion
In physics, equations involving quadratic expressions are frequent. For example, projectile motion often utilizes equations resembling x² - 6, where x represents time or velocity, and the result might represent height or distance. The equation’s properties, such as its roots, reveal key information about the trajectory of the projectile.
3. Optimization Problems
Many optimization problems, whether in engineering, finance, or other fields, involve finding the maximum or minimum values of a function. Analyzing the parabola represented by x² - 6, we can find the minimum value (-6) and understand how changes in x affect the overall result. This can help determine the optimal value of x that produces a desired outcome.
Expanding the Exploration: Variations and Extensions
Let's consider variations on the original theme, leading to richer mathematical discussions.
1. Adding a Constant Term: x² - 6 + c
Adding a constant term 'c' to the expression transforms it into x² - 6 + c. This shifts the parabola vertically by 'c' units. Analyzing how different values of 'c' alter the graph and the roots provides further insight into quadratic functions.
2. Introducing a Linear Term: ax² - 6 + bx
Adding a linear term 'bx' results in a more complex quadratic expression: ax² + bx - 6. The inclusion of 'b' changes the parabola's vertex, axis of symmetry, and roots. This introduces the concept of completing the square and the quadratic formula, powerful tools for solving quadratic equations.
3. Exploring Different Bases: x² - 6 in Different Number Systems
The expression can be explored in various number systems beyond base 10 (decimal). Working with binary, hexadecimal, or other bases adds another layer of complexity and challenges our understanding of numbers and operations.
4. Complex Numbers: Extending the Domain
Expanding the domain of 'x' to include complex numbers opens up further possibilities. When x is a complex number, the expression's values can also be complex, leading to investigations involving the complex plane and its geometric interpretations.
Problem-Solving Strategies: Numerical and Analytical Approaches
Solving problems related to "6 is subtracted from the square of a number" can involve different strategies.
1. Numerical Methods
For finding approximate solutions, numerical methods such as iterative techniques (like the Newton-Raphson method) can be utilized. These methods are particularly useful when dealing with equations that lack simple algebraic solutions.
2. Analytical Methods
Analytical methods, such as factoring, completing the square, and using the quadratic formula, provide exact solutions when applicable. These methods rely on algebraic manipulation to solve for 'x'.
The choice of method depends on the specific problem and the desired level of precision.
Conclusion: A Foundation for Further Learning
The seemingly simple expression, "6 is subtracted from the square of a number," serves as a springboard for a deep dive into various mathematical concepts. From basic algebra and graph interpretation to advanced topics like numerical methods and complex numbers, this phrase unlocks a world of exploration and understanding. It highlights the interconnectedness of different mathematical areas and encourages a deeper appreciation of the power and beauty of mathematics. Further exploration can involve examining higher-order polynomials, investigating related functions, and applying these concepts to diverse fields of study. The journey of mathematical learning is ongoing, and this simple expression provides a valuable starting point.
Latest Posts
Latest Posts
-
Which Of The Following Are Components Of File Handling
Jun 06, 2025
-
There Is A Rope Holding A Piece Of Wood Underwater
Jun 06, 2025
-
All Of The Following Are True For Grievances Except
Jun 06, 2025
-
Cu L Es La Mitad De 500
Jun 06, 2025
-
How Does A Writer Support A Counterclaim After Stating It
Jun 06, 2025
Related Post
Thank you for visiting our website which covers about 6 Is Subtracted From The Square Of A Number. . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.