7 X 4 2 18 10
Breaking News Today
Jun 04, 2025 · 5 min read
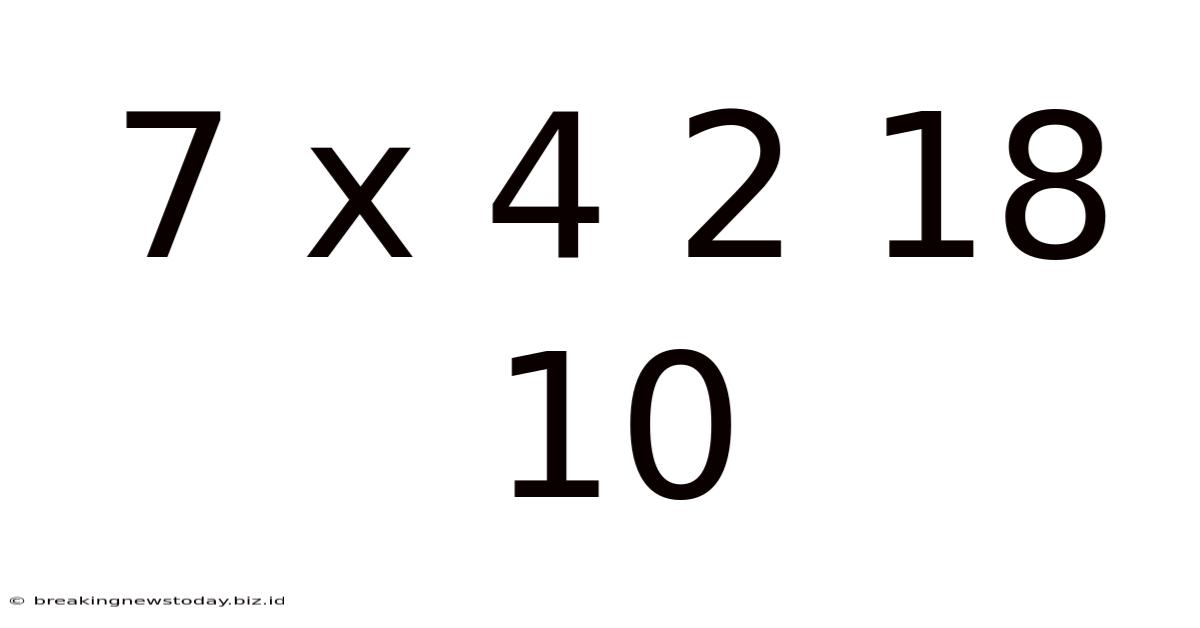
Table of Contents
Decoding the Sequence: 7 x 4 2 18 10 – A Deep Dive into Pattern Recognition and Problem Solving
The seemingly simple sequence "7 x 4 2 18 10" presents a fascinating challenge. At first glance, it appears random. However, by applying principles of pattern recognition, logical reasoning, and creative problem-solving, we can unravel its underlying structure. This exploration delves into various approaches, highlighting the importance of critical thinking and demonstrating the multiple pathways to a solution. This isn't just about finding an answer; it's about understanding the process of finding answers – a crucial skill applicable far beyond this specific numerical puzzle.
The Illusion of Randomness and the Power of Pattern Recognition
Our initial reaction to the sequence "7 x 4 2 18 10" might be one of confusion. The numbers seem disparate, lacking an obvious arithmetic progression. This initial sense of randomness is a common hurdle in problem-solving. Overcoming this requires a shift in perspective – a conscious effort to look beyond the apparent chaos and seek hidden order. This is the core of pattern recognition: identifying underlying relationships or structures within seemingly disorganized data.
Potential Approaches: Exploring Various Mathematical Operations
To decode the sequence, let's explore various mathematical operations and their potential applications:
1. Arithmetic Sequences and Series:
The simplest approach involves examining whether the sequence follows a simple arithmetic progression (addition or subtraction of a constant value) or a geometric progression (multiplication or division by a constant value). In this case, a straightforward arithmetic or geometric pattern is absent. This leads us to explore more complex possibilities.
2. Combinations of Arithmetic and Geometric Progressions:
We could investigate whether a combination of arithmetic and geometric progressions could generate the sequence. For instance, alternating between addition and multiplication or a more intricate interwoven pattern might be possible, but this requires rigorous testing and may not yield a consistent solution.
3. Exploring Non-Linear Relationships:
The sequence might not adhere to linear relationships at all. We need to consider non-linear functions, such as quadratic equations, exponential functions, or more complex mathematical models. Finding such a relationship requires a deeper analysis and potentially advanced mathematical tools. This approach can become computationally intensive without a clear starting point.
4. Hidden Operations and Symbolic Representations:
The "x" symbol in the sequence is intriguing. It might represent a conventional multiplication, or it could symbolize a different operation entirely – a hidden code, a function, or a relationship between the numbers. The ambiguity of the "x" expands the possibilities dramatically.
5. Considering External Factors: Context and Clues
Is there any external context to this sequence? Was it presented as part of a larger problem or puzzle? Often, problems that appear initially random might derive from a specific context or set of rules that are not explicitly stated. Without additional information, this approach is currently limited.
Developing a Framework for Solution: A Step-by-Step Approach
To systematize our search for a pattern, let's adopt a structured approach:
1. Data Representation: Represent the sequence visually. This can involve creating a table, a graph, or a diagram. Visual representation often reveals hidden connections that might be missed in a purely numerical analysis.
2. Hypothesis Generation: Formulate hypotheses about possible patterns. These should be based on the mathematical operations we explored earlier. Each hypothesis should be clearly stated and testable.
3. Hypothesis Testing: Systematically test each hypothesis. This involves applying the proposed pattern to the sequence and evaluating whether it accurately predicts the subsequent numbers. Keep detailed records of your tests.
4. Iterative Refinement: If a hypothesis is incorrect, refine it based on the results of the testing. Don't be afraid to discard hypotheses that don't work. This iterative process is crucial in problem-solving.
5. Verification and Generalization: Once a consistent pattern is identified, verify it by applying it to additional data points if available. If the pattern holds true, attempt to generalize it – can it be applied to similar sequences?
The Importance of Lateral Thinking and Creative Problem Solving
It's crucial to remember that there might be multiple valid solutions, or perhaps no immediately obvious solution. This highlights the importance of lateral thinking – the ability to approach problems from unconventional angles. Don't be afraid to think "outside the box" and explore possibilities that might initially seem illogical.
Exploring Alternative Interpretations of the "x" Symbol:
Perhaps the "x" isn't multiplication. It could represent a different operation, or even a separator between different parts of the sequence. For example:
- Concatenation: The "x" might signify joining numbers. This could lead to a completely different interpretation of the sequence.
- Functional Notation: "x" could represent a function applied to the numbers before and after it. This necessitates defining what this function is.
- Coded Message: The sequence might be a coded message, where each number represents a letter or symbol. This interpretation would necessitate a code-breaking approach.
Advanced Mathematical Techniques:
If simpler approaches fail, advanced mathematical techniques could be applied:
- Regression Analysis: Statistical methods like regression analysis could be used to find a best-fit model for the sequence. This involves finding a mathematical function that minimizes the difference between the predicted and observed values.
- Fourier Analysis: This technique can be used to analyze periodic or cyclical patterns in the data.
Conclusion: The Value of the Process
The puzzle presented by the sequence "7 x 4 2 18 10" is not merely about finding the "right answer". It is a valuable exercise in sharpening critical thinking skills, fostering creativity, and highlighting the importance of systematic problem-solving. The process of exploring different approaches, generating and testing hypotheses, and embracing iterative refinement is more significant than any single solution. The journey of uncovering the underlying pattern is as valuable as the destination itself, equipping us with a powerful arsenal of techniques applicable to a wide range of intellectual challenges. The sequence serves as a microcosm of the broader problem-solving process, demonstrating how seemingly random data can reveal underlying order through persistent investigation and creative thought. This process is applicable to diverse fields, from data analysis to scientific research, highlighting the transferability of analytical skills honed through seemingly simple puzzles.
Latest Posts
Latest Posts
-
Who Lives In A Typical Household In Nicaragua
Jun 05, 2025
-
In Which Career Cluster Are Librarians Classified
Jun 05, 2025
-
Which Two Way Frequency Table Correctly Shows The Marginal Frequencies
Jun 05, 2025
-
Before The Anchor Is Placed In The Hole Workers Should
Jun 05, 2025
-
3 4 Has How Many 1 8 In It
Jun 05, 2025
Related Post
Thank you for visiting our website which covers about 7 X 4 2 18 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.