A Number Is More Than 9 Units From 3
Breaking News Today
Jun 01, 2025 · 6 min read
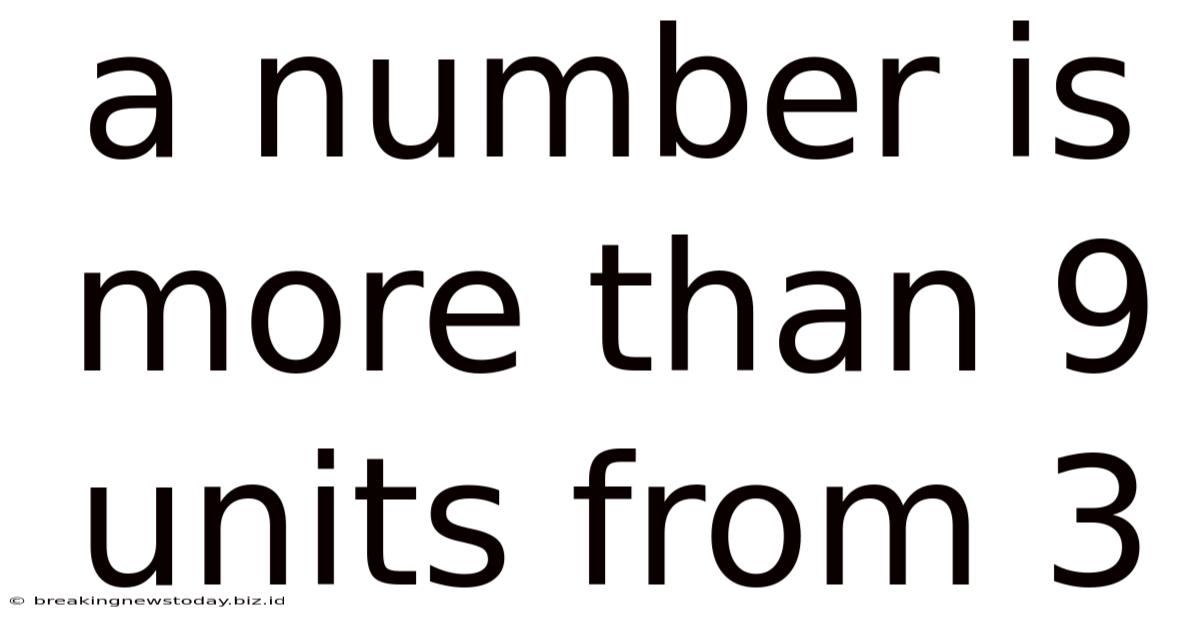
Table of Contents
A Number is More Than 9 Units from 3: Exploring the Mathematical Concept and its Applications
This article delves into the mathematical concept represented by the statement "a number is more than 9 units from 3." We will explore the mathematical representation, solve related problems, and examine its applications in various fields. Understanding this seemingly simple statement unlocks a deeper understanding of inequalities and their practical uses.
Understanding the Mathematical Inequality
The phrase "a number is more than 9 units from 3" translates into a mathematical inequality. Let's represent the unknown number as 'x'. The distance between x and 3 is given by the absolute difference |x - 3|. The statement "more than 9 units" means this distance is greater than 9. Therefore, the inequality is:
|x - 3| > 9
This inequality signifies that the number 'x' lies either more than 9 units to the right of 3 or more than 9 units to the left of 3 on the number line.
Solving the Inequality
To solve this inequality, we need to consider two separate cases:
Case 1: x - 3 > 9
Adding 3 to both sides, we get:
x > 12
This means any number greater than 12 satisfies this condition.
Case 2: x - 3 < -9
Adding 3 to both sides, we get:
x < -6
This means any number less than -6 satisfies this condition.
Therefore, the solution to the inequality |x - 3| > 9 is x > 12 or x < -6. This can be represented on a number line with two distinct intervals: one extending infinitely to the right of 12 and the other extending infinitely to the left of -6.
Visual Representation on the Number Line
A number line provides a clear visual representation of the solution. We mark the points -6 and 12. An open circle at each point indicates that these values are not included in the solution (as the inequality is "greater than," not "greater than or equal to"). The solution is represented by two shaded regions: one to the left of -6 and one to the right of 12.
<-------------------|------------------->
-6 0 12
(Shaded) (Unshaded) (Shaded)
Real-World Applications
The concept of a number being more than a certain distance from a reference point has numerous applications in various fields:
1. Quality Control and Manufacturing
In manufacturing processes, this concept is crucial for quality control. Imagine a machine producing bolts with a target length of 3 cm. If the acceptable deviation (tolerance) is 9 mm (0.9 cm), then any bolt with a length x such that |x - 3| > 0.9 cm is considered defective and needs to be rejected. This ensures that the produced bolts fall within the specified acceptable range.
2. Temperature Control and Monitoring
Consider a thermostat designed to maintain a room temperature of 3°C. If a safety mechanism is triggered when the temperature deviates by more than 9°C from the set point, this scenario is mathematically described by the inequality |x - 3| > 9, where x represents the room temperature. This ensures the system activates a safeguard to prevent potential issues caused by extreme temperature fluctuations.
3. Financial Modeling and Risk Assessment
In finance, this concept is often used in risk management. For instance, if the expected return of an investment is 3%, and a risk threshold is set at a deviation of more than 9 percentage points, then any investment with a return x such that |x - 3| > 9% is deemed too risky and may be avoided. This concept helps manage the level of risk within a portfolio.
4. Physics and Engineering: Tolerance and Error Margins
In many engineering applications, tolerances are crucial. The concept of being more than 9 units away from a target value is directly applicable when dealing with measurements and acceptable errors. For instance, in constructing a bridge, a specific length of steel beams is required. If the allowable margin of error is more than 9 millimeters, then the length x of the steel beams must satisfy an inequality similar to the one we discussed. Any beam failing to meet this condition would be rejected.
5. Statistics and Data Analysis: Outliers Detection
In statistical analysis, this principle is indirectly used to identify outliers. While the specific method for outlier detection might differ, the core idea involves determining whether a data point is significantly distant from the mean or median. The distance from a central value exceeding a certain threshold (like 9 units from a mean in a simplified example) can flag a data point as a potential outlier, requiring further investigation to determine if it's erroneous or truly represents an anomaly.
6. Geographic Applications and Distance Calculations
Imagine you are setting up a communication tower with a range of 9 kilometers. If the tower is located at a point represented by 3 on a coordinate system (simplified for illustrative purposes), then any location x where the distance |x - 3| > 9 kilometers is beyond the communication range of the tower.
Extending the Concept: Variations and Generalizations
The basic concept can be easily generalized. Instead of "9 units from 3," we could consider "k units from a." The inequality would then become:
|x - a| > k
Solving this inequality follows the same process:
- x - a > k => x > a + k
- x - a < -k => x < a - k
Therefore, the solution is x > a + k or x < a - k. This generalized form highlights the versatility of the mathematical concept.
Applications in Computer Science and Programming
The concept finds use in various computer science applications, including:
-
Error Handling and Exception Management: In programming, this principle is implicit in many error-handling routines. For example, if a program expects an input value near a specific target and the difference exceeds a certain threshold, an error is flagged, ensuring program stability.
-
Search Algorithms: In some search algorithms, a "distance" metric is used to identify the closest match to a query. The concept of exceeding a certain distance from a target could be used to prune the search space and improve efficiency by eliminating elements considered too far from the desired result.
-
Data Validation and Filtering: When inputting data, applications often validate the data against specified parameters. If an input is outside an acceptable range (similar to our inequality), it might be rejected or flagged, maintaining data quality.
Conclusion
The seemingly simple statement, "a number is more than 9 units from 3," underpins a powerful mathematical concept with far-reaching applications. By understanding the inequality |x - 3| > 9 and its generalized form |x - a| > k, we can effectively solve related problems and appreciate its significance across various disciplines, from manufacturing and finance to computer science and geographic information systems. The ability to translate real-world scenarios into mathematical inequalities and to interpret the results is a valuable skill in many fields. The versatility of this concept makes it a fundamental building block for more complex mathematical models and problem-solving techniques. Its application extends beyond simple numerical problems to more sophisticated systems and decision-making processes. Mastering this concept provides a strong foundation for further exploration of advanced mathematical principles and their real-world relevance.
Latest Posts
Latest Posts
-
The Details Of This Excerpt Reveal The Authors Purpose By
Jun 02, 2025
-
One Drawback To Performing The Butterfly Method Is The
Jun 02, 2025
-
A Branch Of Chemistry Is Named After Oxygen
Jun 02, 2025
-
Besides Providing Direction Goals In Business Motivate Because They
Jun 02, 2025
-
Factor The Expression Over The Complex Numbers X2 18
Jun 02, 2025
Related Post
Thank you for visiting our website which covers about A Number Is More Than 9 Units From 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.