An Extended Object Is In Static Equilibrium If __________.
Breaking News Today
Mar 28, 2025 · 8 min read
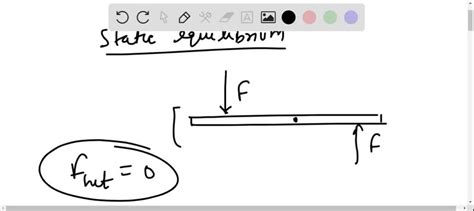
Table of Contents
An Extended Object is in Static Equilibrium If… Net Force and Net Torque Equal Zero!
Understanding static equilibrium is crucial in physics, engineering, and many other fields. It's the foundation for designing stable structures, analyzing forces in stationary systems, and predicting the behavior of rigid bodies at rest. But what exactly defines static equilibrium for an extended object? It's not just about a single point; it's about the entire object's state. This article delves into the conditions required for an extended object to achieve this state of rest, exploring the concepts of net force, net torque, and their crucial role in maintaining balance.
Understanding Extended Objects and Static Equilibrium
Before diving into the specifics, let's clarify some terminology. An extended object is any object that cannot be considered a point mass. Its size and shape are significant factors in analyzing its behavior under the influence of forces. Think of a seesaw, a bridge, or even a complex machine—these are all examples of extended objects.
Static equilibrium describes a state where an object is at rest and remains at rest. This seemingly simple condition requires a precise balance of forces and torques acting upon the object. A key distinction here is between static equilibrium and dynamic equilibrium. While static equilibrium describes an object at rest, dynamic equilibrium describes an object moving at a constant velocity. This article focuses solely on static equilibrium.
The Two Fundamental Conditions for Static Equilibrium
For an extended object to be in static equilibrium, two fundamental conditions must be met simultaneously:
-
The net force acting on the object must be zero. This means that the vector sum of all external forces acting on the object must equal zero. This condition ensures that the object is not accelerating linearly.
-
The net torque acting on the object must be zero. This means that the vector sum of all external torques acting on the object, about any point, must equal zero. This condition ensures that the object is not rotating.
Let's unpack each condition in greater detail:
Condition 1: Zero Net Force (ΣF = 0)
This condition is intuitive. If the net force acting on an object is non-zero, it will accelerate according to Newton's second law (F = ma). This acceleration will inevitably change the object's state of rest, violating the definition of static equilibrium. Therefore, for an extended object to remain stationary, the sum of all forces acting on it in each direction (x, y, and z) must be zero.
This can be expressed mathematically as:
ΣFx = 0 ΣFy = 0 ΣFz = 0
Where:
- ΣFx represents the sum of all forces in the x-direction.
- ΣFy represents the sum of all forces in the y-direction.
- ΣFz represents the sum of all forces in the z-direction.
This means that all forces acting on the object must perfectly balance each other out. For example, if a heavy object is suspended by a rope, the tension in the rope must exactly equal the weight of the object to prevent it from falling.
Condition 2: Zero Net Torque (Στ = 0)
This condition is less intuitive but equally crucial. Torque, or moment of force, is the rotational equivalent of force. It's a measure of how much a force tends to cause rotation around a specific point or axis. Even if the net force on an object is zero, it can still rotate if the net torque is non-zero. This rotation again violates the condition of static equilibrium.
Torque (τ) is calculated as:
τ = r x F
Where:
- r is the distance from the pivot point (or axis of rotation) to the point where the force is applied.
- F is the force.
- x represents the cross product, indicating that only the component of the force perpendicular to the lever arm contributes to the torque.
The net torque must be zero about any point. This is a critical aspect of the condition. If the net torque is zero about one point, it will be zero about all points, provided the net force is also zero. Choosing a convenient pivot point simplifies calculations significantly.
To ensure static equilibrium, the sum of all clockwise torques must equal the sum of all counterclockwise torques around any chosen point. This guarantees that there is no net rotational motion.
Practical Applications and Examples
The principles of static equilibrium are fundamental to various real-world applications:
-
Structural Engineering: Architects and engineers rely heavily on these principles to design stable bridges, buildings, and other structures. The forces acting on each structural element must be balanced to prevent collapse.
-
Mechanical Engineering: Designing machines and mechanisms necessitates a thorough understanding of static equilibrium. The forces and torques on gears, levers, and other components must be meticulously analyzed to ensure stable operation.
-
Robotics: Maintaining the stability of robots is critical for their safe and effective operation. Static equilibrium analysis ensures that the robot remains upright and does not tip over, even under varying loads and movements.
-
Physics Experiments: Many physics experiments rely on precise balancing of forces and torques to achieve desired outcomes. For example, the classic experiment involving a meter stick balanced on a fulcrum demonstrates the conditions for static equilibrium visually.
Example 1: A Simple Seesaw
A classic example is a seesaw. For the seesaw to be balanced (in static equilibrium), the following conditions must hold:
-
Zero Net Force: The downward force due to the weight of the children on each side must be balanced by the upward force exerted by the fulcrum.
-
Zero Net Torque: The clockwise torque exerted by one child must equal the counterclockwise torque exerted by the other child. This depends on both their weights and their distances from the fulcrum.
Example 2: A Ladder Leaning Against a Wall
Consider a ladder leaning against a wall. The ladder is in static equilibrium when the following are balanced:
-
Zero Net Force: The weight of the ladder (acting downwards) is balanced by the normal forces from the wall and the ground (acting upwards and outwards respectively). Friction between the ladder and the ground, as well as the wall also plays a role.
-
Zero Net Torque: The torques due to the weight of the ladder and the reaction forces at the wall and the ground must balance out around any point, typically the base of the ladder. The chosen point often simplifies the calculations.
Example 3: A Hanging Sign
A sign hanging from a horizontal beam is a common example. For the sign to be static, the following must be met:
-
Zero Net Force: The downward force due to the weight of the sign is balanced by the tension in the support wires/ropes.
-
Zero Net Torque: The torques created by the weight of the sign and the tension in each support must cancel each other out at any point along the beam. This would likely involve resolving the tension in the wires into horizontal and vertical components and taking torques around a convenient point.
Solving Static Equilibrium Problems
Solving static equilibrium problems often involves using free-body diagrams and applying the conditions of zero net force and zero net torque. A free-body diagram illustrates all the forces acting on an object, allowing for a systematic analysis of their magnitudes and directions. The choice of pivot point in the torque calculation is often strategically made to eliminate unnecessary variables, simplifying the problem greatly.
The process typically involves these steps:
-
Draw a free-body diagram: Represent the object and all external forces acting on it.
-
Choose a coordinate system: Define the x, y, and z directions.
-
Resolve forces into components: Break down forces into their x, y, and z components.
-
Apply the condition of zero net force: Set up equations for ΣFx = 0, ΣFy = 0, and ΣFz = 0.
-
Choose a pivot point: Select a point for calculating torques (often a point where an unknown force acts).
-
Apply the condition of zero net torque: Set up an equation for Στ = 0.
-
Solve the system of equations: Solve the simultaneous equations to determine the unknown forces or torques.
Advanced Considerations
While the basic principles of static equilibrium are relatively straightforward, more complex situations may involve:
-
Distributed Loads: Instead of concentrated forces, objects may experience forces spread over an area (e.g., the weight of a beam distributed along its length).
-
Multiple Connected Bodies: Systems often involve multiple objects interacting with each other (e.g., a system of pulleys and weights).
-
Three-Dimensional Analysis: In some cases, analysis in three dimensions is necessary to fully account for all forces and torques.
These advanced situations require more sophisticated techniques, including integration for distributed loads and considering interaction forces between connected bodies.
Conclusion
An extended object is in static equilibrium if, and only if, the net force and the net torque acting on it are both zero. This fundamental principle underpins the stability of countless structures, machines, and systems in the world around us. Understanding the conditions of static equilibrium, along with the ability to apply free-body diagrams and solve systems of equations, is essential for anyone working in fields that involve force analysis, design, and stability. This knowledge forms the bedrock of understanding how the world around us, in its stationary state, remains stable and unwavering.
Latest Posts
Latest Posts
-
Adam Smiths Invisible Hand Refers To Quizlet
Mar 31, 2025
-
Cvs Does Not Currently Bill Medicare Part B For Quizlet
Mar 31, 2025
-
Dwi With A Passenger Under 15 Is
Mar 31, 2025
-
A Patient With Copd On Positive Pressure Ventilation Quizlet
Mar 31, 2025
-
An Increase In The Real Interest Rate Will Quizlet
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about An Extended Object Is In Static Equilibrium If __________. . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
