Divide 2x2 + 17x + 35 By X + 5.
Breaking News Today
Jun 05, 2025 · 5 min read
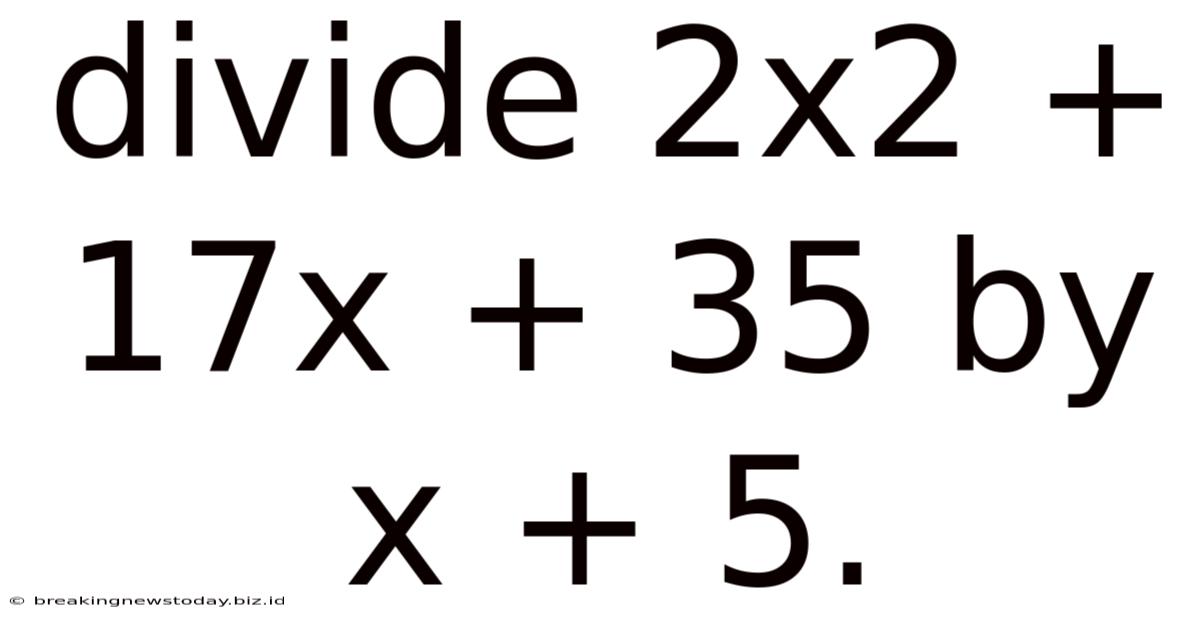
Table of Contents
Dividing 2x² + 17x + 35 by x + 5: A Comprehensive Guide
Polynomial division can seem daunting, but with a systematic approach, it becomes manageable and even enjoyable. This article will walk you through the process of dividing the polynomial 2x² + 17x + 35 by the binomial x + 5, exploring various methods and highlighting key concepts. We’ll go beyond just finding the answer; we'll delve into the underlying principles and explore how this process relates to other areas of algebra.
Understanding Polynomial Division
Before we dive into the specifics of our problem, let's establish a foundational understanding of polynomial division. Essentially, it's the process of determining how many times one polynomial (the divisor) goes into another polynomial (the dividend). The result is called the quotient, and any remaining portion is the remainder. This process is analogous to long division with numbers.
Key Terminology:
- Dividend: The polynomial being divided (in our case, 2x² + 17x + 35).
- Divisor: The polynomial doing the dividing (in our case, x + 5).
- Quotient: The result of the division.
- Remainder: Any part of the dividend that's left over after the division.
Method 1: Long Division
Long division is a classic and reliable method for polynomial division. Let's apply it to our problem:
(2x² + 17x + 35) ÷ (x + 5)
-
Set up the long division:
________________ x + 5 | 2x² + 17x + 35 -
Divide the leading term of the dividend by the leading term of the divisor:
2x² ÷ x = 2x
Write this above the dividend:
2x ________________ x + 5 | 2x² + 17x + 35 -
Multiply the quotient term (2x) by the divisor (x + 5):
2x(x + 5) = 2x² + 10x
Write this below the dividend:
2x ________________ x + 5 | 2x² + 17x + 35 2x² + 10x -
Subtract the result from the dividend:
(2x² + 17x + 35) - (2x² + 10x) = 7x + 35
2x ________________ x + 5 | 2x² + 17x + 35 2x² + 10x -------- 7x + 35 -
Bring down the next term (35):
2x ________________ x + 5 | 2x² + 17x + 35 2x² + 10x -------- 7x + 35 -
Repeat steps 2-5:
7x ÷ x = 7
2x + 7 ________________ x + 5 | 2x² + 17x + 35 2x² + 10x -------- 7x + 35 7x + 35 -------- 0 -
The remainder is 0.
Therefore, (2x² + 17x + 35) ÷ (x + 5) = 2x + 7
Method 2: Synthetic Division
Synthetic division is a shortcut method for dividing polynomials, particularly useful when the divisor is of the form (x - c), where 'c' is a constant. Let's use synthetic division for our problem:
Since our divisor is x + 5, c = -5.
-
Write down the coefficients of the dividend: 2, 17, 35
-
Bring down the first coefficient:
-5 | 2 17 35 | -------- 2 -
Multiply the brought-down coefficient by c (-5) and add it to the next coefficient:
-5 | 2 17 35 | -10 -------- 2 7 -
Repeat step 3:
-5 | 2 17 35 | -10 -35 -------- 2 7 0
The last number (0) is the remainder. The other numbers are the coefficients of the quotient.
Therefore, the quotient is 2x + 7, and the remainder is 0.
Method 3: Factoring
Factoring is a powerful technique that can sometimes simplify polynomial division, especially when the divisor is a factor of the dividend. Let's factor the dividend:
2x² + 17x + 35
We're looking for two numbers that add up to 17 and multiply to 2 * 35 = 70. These numbers are 10 and 7. We can rewrite the quadratic as:
2x² + 10x + 7x + 35
Now, factor by grouping:
2x(x + 5) + 7(x + 5)
Factor out (x + 5):
(x + 5)(2x + 7)
Now we can see that (x + 5) is a factor of 2x² + 17x + 35. Dividing (x+5)(2x+7) by (x+5) leaves us with 2x + 7.
Comparing the Methods
All three methods—long division, synthetic division, and factoring—yield the same result: 2x + 7. The best method depends on the specific problem and your comfort level with each technique.
- Long division: Always works, regardless of the divisor's form. It's a systematic approach, good for understanding the fundamentals.
- Synthetic division: A faster method when the divisor is of the form (x - c). It's less prone to arithmetic errors than long division.
- Factoring: The most efficient if the divisor is a factor of the dividend. It relies on recognizing factors, which might not always be straightforward.
Applications of Polynomial Division
Polynomial division isn't just an abstract mathematical exercise; it has practical applications in various fields:
- Calculus: Finding derivatives and integrals of rational functions often involves polynomial division.
- Engineering: Solving equations and modeling systems often requires manipulating polynomials, and division is a crucial tool.
- Computer Science: Polynomial division algorithms are used in computer graphics, signal processing, and cryptography.
- Economics and Finance: Modeling economic growth, analyzing financial data, and forecasting trends might involve polynomial equations requiring division.
Further Exploration: Remainder Theorem
The remainder theorem states that when a polynomial f(x) is divided by (x - c), the remainder is f(c). In our example, f(x) = 2x² + 17x + 35, and c = -5.
f(-5) = 2(-5)² + 17(-5) + 35 = 50 - 85 + 35 = 0
The remainder is 0, confirming our previous results. This theorem provides a quick way to check the remainder without performing the full division.
Conclusion
Dividing 2x² + 17x + 35 by x + 5 results in a quotient of 2x + 7 and a remainder of 0. We’ve explored three different methods to achieve this result, highlighting their strengths and weaknesses. Polynomial division is a fundamental algebraic skill with far-reaching applications across various disciplines. Mastering this concept lays a solid foundation for more advanced mathematical concepts and problem-solving in numerous fields. Remember to practice regularly and choose the method that best suits your needs and the complexity of the problem. By understanding the underlying principles and applying the appropriate techniques, you can confidently tackle polynomial division problems of any level.
Latest Posts
Latest Posts
-
Which Factors Cause Weather Patterns Check All That Apply
Jun 06, 2025
-
Enlightenment Philosophers Established Which Two Of The Following Ideas
Jun 06, 2025
-
Select The Sketches Of A 3d Orbital
Jun 06, 2025
-
Which Is Not An Element Of An Acceptable Id
Jun 06, 2025
-
The Following Should Not Be Done On An Expressway
Jun 06, 2025
Related Post
Thank you for visiting our website which covers about Divide 2x2 + 17x + 35 By X + 5. . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.