Evaluate 5 X 1 2 When X 3
Breaking News Today
Jun 07, 2025 · 4 min read
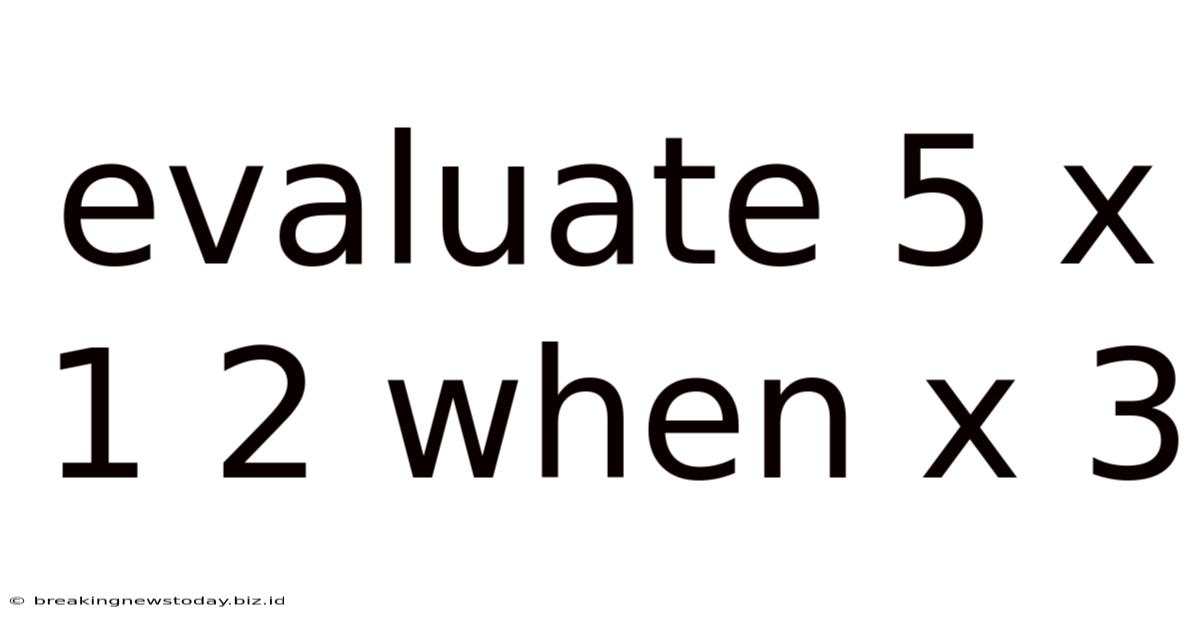
Table of Contents
Evaluating 5x + 12 When x = 3: A Comprehensive Guide
This article will delve into the seemingly simple, yet fundamentally important, mathematical process of evaluating algebraic expressions. We'll focus specifically on evaluating the expression 5x + 12 when x = 3. While the solution might appear straightforward, understanding the underlying principles is crucial for mastering more complex algebraic concepts. We'll explore not only the calculation itself but also the broader context of algebraic substitution and its applications in various fields.
Understanding Algebraic Expressions
An algebraic expression is a mathematical phrase that combines numbers, variables, and operators (like +, -, ×, ÷). Variables, usually represented by letters like x, y, or z, represent unknown values. The expression 5x + 12 contains the variable 'x', the constant term '12', and the operators '+' (addition) and '×' (implied multiplication between 5 and x). The '5' is called the coefficient of 'x'.
The Concept of Substitution
Substituting a value for a variable involves replacing the variable with the given value. This allows us to evaluate the expression and obtain a numerical result. In our example, we are given that x = 3. This means we will replace every instance of 'x' in the expression 5x + 12 with the number 3.
Step-by-Step Evaluation of 5x + 12 when x = 3
Let's break down the evaluation process step-by-step:
-
Substitution: Replace 'x' with '3' in the expression 5x + 12. This gives us: 5(3) + 12.
-
Multiplication: Perform the multiplication operation first, following the order of operations (PEMDAS/BODMAS). 5 multiplied by 3 is 15. Our expression now becomes: 15 + 12.
-
Addition: Finally, perform the addition. 15 plus 12 equals 27.
Therefore, the value of the expression 5x + 12 when x = 3 is 27.
Verification and Practice Problems
It's always good practice to verify your answer. You can do this by trying different methods or checking your work meticulously. Let's try a slightly different approach:
- We can rearrange the expression: 5x + 12 can be written as 5(x) + 12. Substituting x = 3, we get 5(3) + 12 = 15 + 12 = 27. The result remains the same.
Here are some practice problems to solidify your understanding:
- Evaluate 2x - 7 when x = 5.
- Evaluate 3y² + 4y - 1 when y = 2.
- Evaluate (4z + 6)/2 when z = 1.
- Evaluate -x² + 5x - 2 when x = -1.
- Evaluate √(x + 9) when x = 7.
Solutions (Hidden for self-checking):
<details> <summary>Click to reveal solutions</summary>
- 3
- 19
- 5
- -8
- 4 </details>
Real-World Applications of Algebraic Substitution
The ability to substitute values into algebraic expressions is a cornerstone of many fields:
-
Physics: Calculating velocity, acceleration, or force using equations involving variables like time, mass, and distance. For example, if we know the acceleration (a) and time (t), we can use the equation v = u + at (where v is final velocity and u is initial velocity) to find the final velocity.
-
Engineering: Determining the stress on a material, the current flow in a circuit, or the power output of a machine, all often require substituting known values into appropriate formulas.
-
Economics: Modeling economic relationships, predicting market trends, and calculating profits or losses using equations that incorporate variables like price, quantity, and cost.
-
Computer Science: Programming algorithms and writing code frequently involves using variables and performing substitutions to manipulate data and achieve desired outcomes.
-
Chemistry: Calculating the concentration of a solution, the amount of reactants needed for a chemical reaction, or determining the yield of a product using stoichiometric calculations that involve substituting known values into chemical formulas and equations.
Advanced Concepts and Extensions
While our focus has been on a relatively simple expression, the principle of substitution extends to more intricate scenarios:
-
Functions: A function is a relationship that assigns each input value (x) to a unique output value (y). Evaluating a function at a specific point involves substituting the input value into the function's definition to find the corresponding output.
-
Systems of Equations: Solving systems of equations often involves substituting the value of one variable found in one equation into another equation to solve for the remaining variables.
-
Calculus: Substitution is fundamental in integral and differential calculus, where it is used to simplify complex expressions and solve integration problems.
Conclusion: Mastering the Fundamentals
Evaluating algebraic expressions through substitution is a foundational skill in mathematics and its many applications. While the example of 5x + 12 when x = 3 might seem elementary, mastering this process builds a strong base for tackling increasingly complex mathematical challenges. Understanding the concepts of variables, coefficients, operators, and the order of operations is crucial. Regular practice and exploring real-world applications will further solidify your understanding and empower you to solve a wide range of problems. Remember to break down complex problems into smaller, manageable steps, and always verify your answers. With consistent effort, you can achieve proficiency in algebraic manipulation and confidently apply these skills to diverse fields.
Latest Posts
Latest Posts
-
To What Aspects Does Iconography Pertain
Jun 07, 2025
-
Exotic Collectibles Is An International Business As Such It
Jun 07, 2025
-
Links An Electric Meter To A Local Utility
Jun 07, 2025
-
Given 1 And 2 Are Supplements
Jun 07, 2025
-
7 02 Is 10 4 Of What Number
Jun 07, 2025
Related Post
Thank you for visiting our website which covers about Evaluate 5 X 1 2 When X 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.