Factor 12y + 6 Using The Gcf
Breaking News Today
Jun 04, 2025 · 5 min read
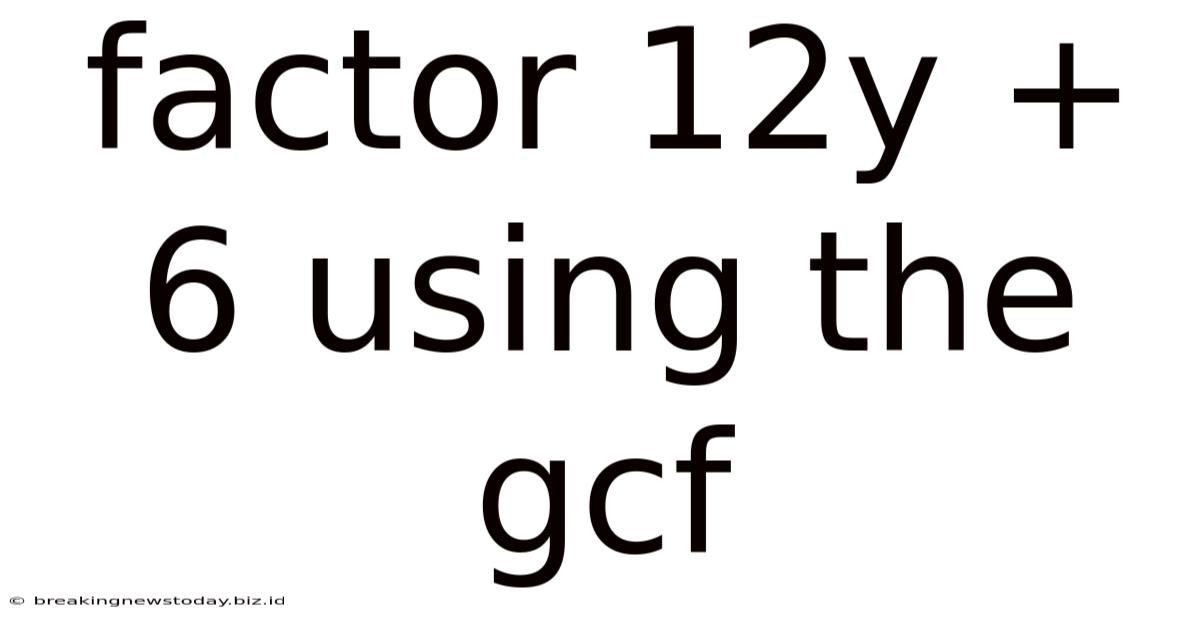
Table of Contents
Factoring 12y + 6 Using the GCF: A Comprehensive Guide
Factoring algebraic expressions is a fundamental skill in algebra. It's the process of breaking down a complex expression into simpler components, much like finding the prime factors of a number. This article will delve deeply into factoring the expression 12y + 6 using the greatest common factor (GCF), explaining the process step-by-step and exploring related concepts to solidify your understanding. We'll also touch upon why this skill is crucial and its applications in higher-level mathematics.
Understanding the Greatest Common Factor (GCF)
Before we tackle factoring 12y + 6, let's clarify what the greatest common factor is. The GCF of two or more numbers (or terms in an algebraic expression) is the largest number that divides evenly into all of them without leaving a remainder. For example, the GCF of 12 and 6 is 6 because 6 is the largest number that divides both 12 and 6 without leaving a remainder.
Finding the GCF involves identifying the prime factors of each number. Prime factors are numbers greater than 1 that are only divisible by 1 and themselves (e.g., 2, 3, 5, 7, 11, etc.).
Let's find the GCF of 12 and 6:
- 12: The prime factorization of 12 is 2 x 2 x 3 (or 2² x 3).
- 6: The prime factorization of 6 is 2 x 3.
Comparing the prime factorizations, we see that both 12 and 6 share a 2 and a 3. Therefore, the GCF of 12 and 6 is 2 x 3 = 6.
Factoring 12y + 6: A Step-by-Step Approach
Now, let's apply this concept to factoring the algebraic expression 12y + 6. Notice that both terms, 12y and 6, contain numerical coefficients. We'll need to find the GCF of these coefficients.
Step 1: Find the GCF of the coefficients.
As we've already established, the GCF of 12 and 6 is 6.
Step 2: Divide each term by the GCF.
- 12y ÷ 6 = 2y
- 6 ÷ 6 = 1
Step 3: Rewrite the expression.
The factored expression will be the GCF multiplied by the results from Step 2, enclosed in parentheses:
6(2y + 1)
Therefore, the factored form of 12y + 6 using the GCF is 6(2y + 1).
Verification: Expanding the Factored Expression
To verify that our factoring is correct, we can expand the factored expression using the distributive property (also known as the FOIL method, for First, Outer, Inner, Last, when dealing with binomials).
6(2y + 1) = 6 * 2y + 6 * 1 = 12y + 6
This confirms that our factored expression, 6(2y + 1), is equivalent to the original expression, 12y + 6.
Beyond the Basics: Factoring with Variables
The principles of GCF factoring extend to expressions containing variables. Let's consider a slightly more complex example: 15x² + 25x
Step 1: Identify the GCF of the coefficients and variables.
- Coefficients: The GCF of 15 and 25 is 5.
- Variables: Both terms contain 'x', and the lowest power of x is x¹. Therefore, the GCF of the variables is x.
The overall GCF is 5x.
Step 2: Divide each term by the GCF.
- 15x² ÷ 5x = 3x
- 25x ÷ 5x = 5
Step 3: Rewrite the expression.
The factored expression is: 5x(3x + 5)
Again, we can verify this by expanding: 5x(3x + 5) = 15x² + 25x
Practical Applications of Factoring
Factoring algebraic expressions, especially using the GCF, is a cornerstone skill in algebra and beyond. Here are some key applications:
-
Solving quadratic equations: Many quadratic equations (equations of the form ax² + bx + c = 0) can be solved by factoring. Factoring simplifies the equation, making it easier to find the values of 'x' that satisfy the equation.
-
Simplifying rational expressions: Rational expressions are fractions containing algebraic expressions. Factoring the numerator and denominator often allows for simplification by canceling common factors.
-
Graphing quadratic functions: The factored form of a quadratic function reveals the x-intercepts (where the graph crosses the x-axis), providing valuable information for graphing the function accurately.
-
Calculus: Factoring is crucial in calculus for techniques like finding derivatives and integrals.
-
Real-world problem-solving: Many real-world problems, particularly those involving optimization or modeling, can be expressed mathematically using quadratic equations or other algebraic expressions. Factoring provides a powerful tool for solving these problems.
Advanced Factoring Techniques
While GCF factoring is a fundamental technique, it's not the only method. Other common factoring techniques include:
-
Difference of squares: This technique applies to expressions of the form a² - b², which factors to (a + b)(a - b).
-
Trinomial factoring: This involves factoring expressions with three terms, often quadratic expressions.
-
Grouping: This method is used for expressions with four or more terms, where you group terms with common factors and then factor further.
Mastering these advanced techniques builds upon the foundational understanding established through GCF factoring.
Troubleshooting Common Mistakes
Several common mistakes can arise when factoring using the GCF:
-
Not finding the greatest common factor: Carefully examine the coefficients and variables to ensure you've identified the largest common factor.
-
Incorrect division: Double-check your division to avoid errors in the remaining terms within the parentheses.
-
Forgetting to include the GCF: The GCF is a crucial part of the factored expression; don't omit it.
-
Improper application of distributive property: When verifying your work, carefully use the distributive property to expand the factored expression and ensure it matches the original expression.
Conclusion: Mastering GCF Factoring
Factoring algebraic expressions using the greatest common factor is an essential skill in algebra and a stepping stone to more advanced mathematical concepts. By systematically following the steps outlined in this guide, practicing regularly with various examples, and understanding the underlying principles, you can confidently master this technique and apply it to a wide range of mathematical problems. Remember to always verify your work by expanding the factored expression to ensure its equivalence to the original expression. The more you practice, the quicker and more intuitive the process will become. Good luck and happy factoring!
Latest Posts
Latest Posts
-
A Container Holds 6 Gallons Of Water
Jun 06, 2025
-
Which Point Requires Correction Regarding The Use Of Restraints
Jun 06, 2025
-
After Identifying Your Talents Passions And Values Write
Jun 06, 2025
-
What Percent Of 21 5 Is 55 04
Jun 06, 2025
-
What Do These Stage Directions Help The Reader Understand
Jun 06, 2025
Related Post
Thank you for visiting our website which covers about Factor 12y + 6 Using The Gcf . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.