Half Of A Number Decreased By 8 Is 3
Breaking News Today
Jun 08, 2025 · 4 min read
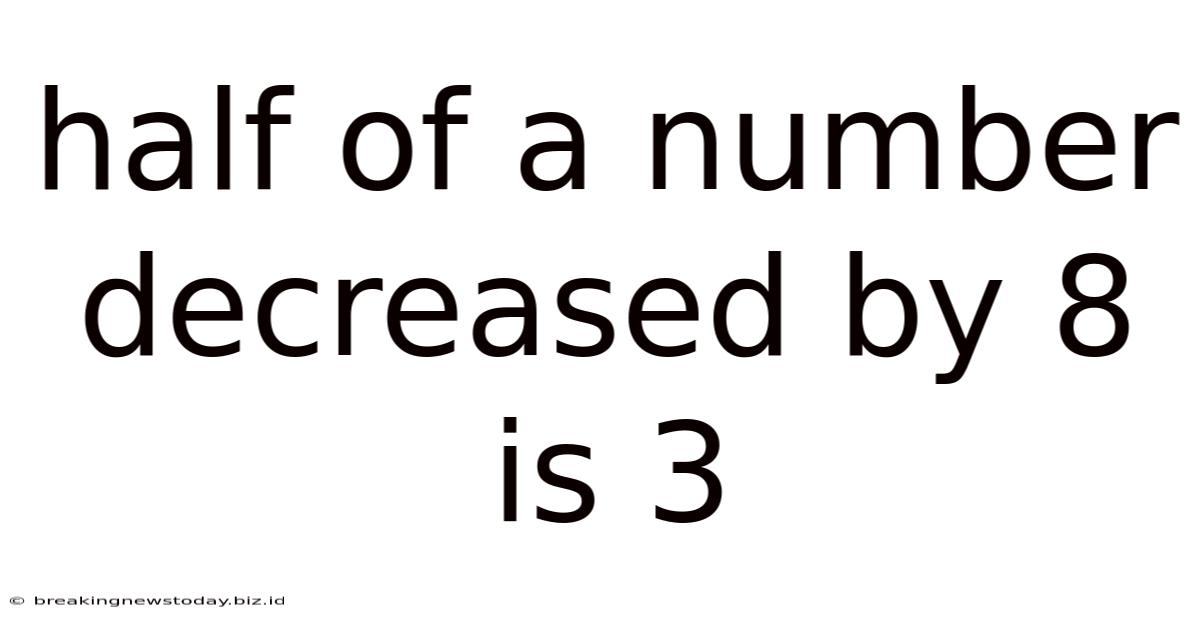
Table of Contents
Half of a Number Decreased by 8 is 3: A Deep Dive into Problem Solving
This seemingly simple math problem, "Half of a number decreased by 8 is 3," opens a door to a world of mathematical concepts and problem-solving strategies. While the solution itself is straightforward, exploring the underlying principles reveals valuable insights applicable to more complex algebraic equations. This article will delve into solving this problem, examining different approaches, and expanding on related concepts to enhance your mathematical understanding.
Understanding the Problem: Translating Words into Equations
The core of successfully tackling this problem lies in accurately translating the English sentence into a mathematical equation. Let's break down each part:
-
"Half of a number": This translates directly to ½x or x/2, where 'x' represents the unknown number.
-
"Decreased by 8": This signifies subtraction; we subtract 8 from the previous expression: ½x - 8
-
"is 3": This indicates equality; the entire expression equals 3: ½x - 8 = 3
Therefore, our word problem is concisely represented by the algebraic equation: ½x - 8 = 3
Solving the Equation: Multiple Approaches
We can solve this equation using several methods, each offering a slightly different perspective on algebraic manipulation.
Method 1: Isolating the Variable
This is the most straightforward approach. Our goal is to isolate 'x' on one side of the equation.
-
Add 8 to both sides: This eliminates the -8 on the left side, leaving us with ½x = 11
-
Multiply both sides by 2: This removes the fraction, isolating 'x': x = 22
Therefore, the number is 22.
Method 2: Clearing the Fraction First
Some prefer eliminating the fraction initially.
-
Multiply both sides by 2: This clears the fraction, resulting in x - 16 = 6
-
Add 16 to both sides: This isolates 'x', giving us x = 22
Again, we arrive at the solution: x = 22
Method 3: Using Inverse Operations
This method emphasizes the concept of inverse operations to undo the actions performed on 'x'.
-
Undo the subtraction: Add 8 to both sides (½x - 8 + 8 = 3 + 8) resulting in ½x = 11
-
Undo the division: Multiply both sides by 2 (½x * 2 = 11 * 2) resulting in x = 22
This approach reinforces the fundamental principles of algebraic manipulation.
Verifying the Solution
It's crucial to verify our solution. Substitute x = 22 back into the original equation:
½(22) - 8 = 11 - 8 = 3
The equation holds true, confirming that our solution, x = 22, is correct.
Expanding on the Concepts: Building a Stronger Foundation
This simple problem provides a springboard to explore more advanced mathematical concepts.
Understanding Variables and Equations
The problem introduces the concept of a variable, represented by 'x', an unknown quantity we need to determine. The equation itself is a statement of equality, asserting that two expressions are equivalent. Mastering the manipulation of variables and equations is fundamental to algebra and beyond.
The Importance of Order of Operations (PEMDAS/BODMAS)
While not explicitly demonstrated in this simple equation, understanding the order of operations (Parentheses/Brackets, Exponents/Orders, Multiplication and Division, Addition and Subtraction) is critical for solving more complex equations. Following the correct order ensures accurate calculations.
Solving More Complex Equations
The techniques used to solve this equation are applicable to more complex algebraic expressions. By understanding how to isolate variables and use inverse operations, you can tackle equations with multiple variables, fractions, decimals, and even exponents.
Applications in Real-World Scenarios
Mathematical equations are not just abstract concepts; they are powerful tools for modeling and solving real-world problems. This simple equation, while seemingly basic, represents the foundation for solving many practical problems in various fields, including:
- Physics: Calculating velocities, accelerations, and forces.
- Engineering: Designing structures and systems.
- Finance: Calculating interest, profits, and losses.
- Computer Science: Developing algorithms and programs.
Problem Solving Strategies: Beyond the Equation
Beyond the mechanics of solving the equation, this problem highlights several valuable problem-solving strategies:
-
Breaking Down the Problem: Deconstructing the word problem into smaller, manageable parts makes it easier to translate into a mathematical equation.
-
Visualizing the Problem: While not necessary for this particular problem, visualizing the problem (e.g., using diagrams or graphs) can be helpful in more complex scenarios.
-
Checking Your Work: Always verify your solution by substituting it back into the original equation or problem statement to ensure accuracy. This builds confidence and prevents errors.
-
Persistence and Patience: Problem-solving is an iterative process. Don't be discouraged by initial difficulties; persistence and a patient approach are key to success.
Conclusion: Mastering the Fundamentals
The seemingly simple problem, "Half of a number decreased by 8 is 3," provides a valuable entry point into the world of algebra and problem-solving. By understanding the underlying principles, mastering the techniques for solving equations, and practicing various problem-solving strategies, you'll build a strong foundation for tackling more complex mathematical challenges. Remember, the key is not just finding the answer (which is 22), but also understanding the process and the concepts involved. This understanding will serve you well in future mathematical endeavors and in applying mathematical reasoning to diverse real-world problems. Keep practicing, and you'll find yourself becoming increasingly confident and proficient in your mathematical abilities.
Latest Posts
Latest Posts
-
Which Statement About The Structure Of English Orthography Is True
Jun 08, 2025
-
Certain Odors Can Initiate Behavioral And Emotional Reactions Because
Jun 08, 2025
-
Which Scatterplot Shows The Strongest Negative Linear Association
Jun 08, 2025
-
Which Model Represents The Factors Of 4x2 9
Jun 08, 2025
-
What Is The Opposite Of The Following Word Contento
Jun 08, 2025
Related Post
Thank you for visiting our website which covers about Half Of A Number Decreased By 8 Is 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.