If Fghi Is A Square Solve For X
Breaking News Today
Jun 02, 2025 · 6 min read
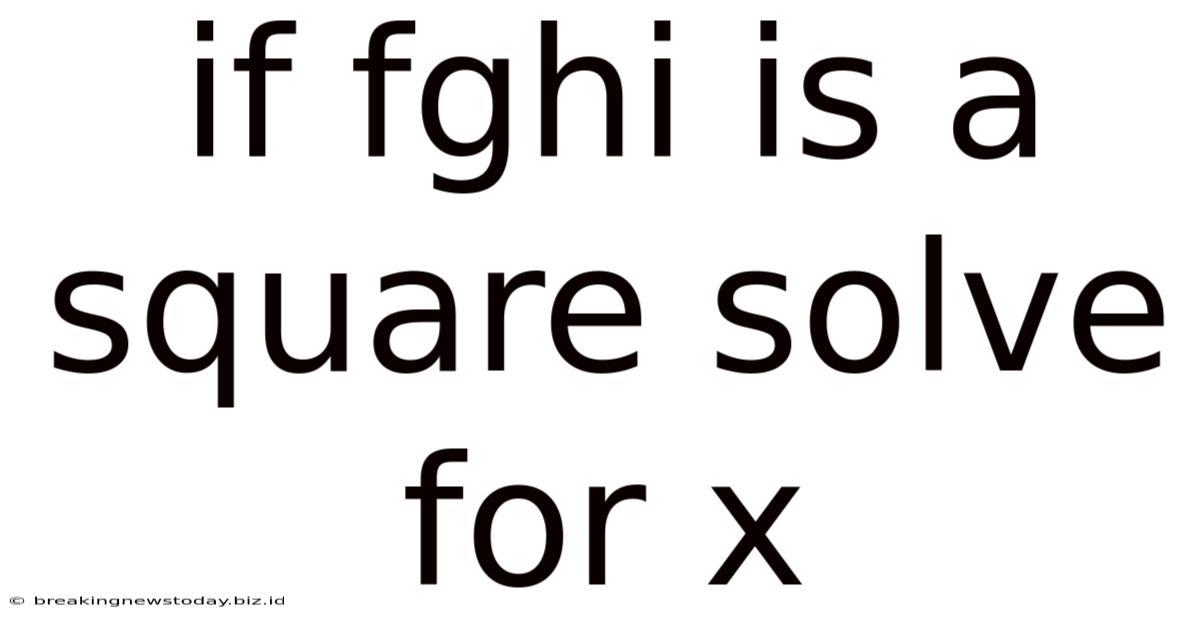
Table of Contents
Decoding the Square: Solving for 'x' in FGHI
This article delves deep into the fascinating world of geometry, specifically focusing on how to solve for an unknown variable, 'x', within the context of a square, FGHI. We'll explore various scenarios, employing different geometrical principles and algebraic techniques to arrive at the solution. Understanding the properties of squares is fundamental to this process, and we’ll cover those in detail before tackling specific problem examples. Prepare to sharpen your problem-solving skills and enhance your understanding of geometrical applications.
Understanding the Properties of a Square
Before we embark on solving for 'x', it’s crucial to revisit the defining properties of a square:
- Four Equal Sides: A square possesses four sides of equal length. This is the cornerstone of many square-related problems.
- Four Right Angles: Each of the four interior angles measures exactly 90 degrees. This property is instrumental in applying trigonometric functions and Pythagorean theorem if needed.
- Equal Diagonals: The diagonals of a square are equal in length and bisect each other at a 90-degree angle. This characteristic often provides additional equations to solve for unknowns.
- Parallel Sides: Opposite sides of a square are parallel to each other. This property is important when considering vectors or translations.
Different Scenarios and Solutions for 'x'
The method for solving for 'x' in a square FGHI varies depending on the information provided. Let's explore several scenarios:
Scenario 1: Side Lengths and 'x'
Let's assume that one side of square FGHI is represented by an algebraic expression involving 'x', and the length of another side is given numerically.
Problem: If FG = 2x + 3 and GH = 7, solve for x.
Solution:
Since FGHI is a square, all its sides are equal. Therefore, FG = GH. We can set up the equation:
2x + 3 = 7
Subtracting 3 from both sides:
2x = 4
Dividing both sides by 2:
x = 2
Therefore, the value of x is 2.
Scenario 2: Diagonal and Side Length
Here, we involve the diagonal of the square and a side length expression containing 'x'.
Problem: The diagonal of square FGHI is 10, and one side (FG) is represented by 5x. Solve for x.
Solution:
We'll use the Pythagorean theorem here. The diagonal of a square forms a right-angled triangle with two adjacent sides. Let's consider the triangle FGH. By the Pythagorean theorem:
FG² + GH² = FH²
Since FG = GH = 5x and FH = 10, we get:
(5x)² + (5x)² = 10²
25x² + 25x² = 100
50x² = 100
x² = 2
x = √2
Therefore, the value of x is the square root of 2.
Scenario 3: Area and Side Length
This scenario uses the area of the square and an expression for side length to solve for 'x'.
Problem: The area of square FGHI is 64 square units, and the side length FG is represented by 2x – 4. Solve for x.
Solution:
The area of a square is calculated by squaring the side length:
Area = side²
Substituting the given values:
(2x – 4)² = 64
Taking the square root of both sides:
2x – 4 = ±8
This gives us two possible equations:
2x – 4 = 8 or 2x – 4 = -8
Solving each equation separately:
2x = 12 => x = 6
2x = -4 => x = -2
Since a side length cannot be negative, we discard x = -2. Therefore, the value of x is 6.
Scenario 4: Perimeter and Side Length
The perimeter of a square is four times the length of one side. This can also be used to solve for x.
Problem: The perimeter of square FGHI is 36 units, and one side FG is represented by 3x + 3. Solve for x.
Solution:
The perimeter of a square is 4 * side length. Therefore:
4(3x + 3) = 36
Dividing both sides by 4:
3x + 3 = 9
Subtracting 3 from both sides:
3x = 6
Dividing both sides by 3:
x = 2
Thus, the value of x is 2.
Scenario 5: Incorporating Trigonometry
More complex problems might incorporate trigonometry, especially when dealing with angles and diagonals. Let’s consider a scenario involving a triangle formed by the diagonal and sides.
Problem: In square FGHI, the diagonal FH forms an angle of θ with side FG. If tan(θ) = 3/4 and FG = 4x, find the value of x.
Solution:
In right-angled triangle FGH, we have:
tan(θ) = Opposite / Adjacent = GH / FG
Given that tan(θ) = 3/4 and FG = 4x, and since GH = FG in a square:
3/4 = 4x / 4x
This equation simplifies to 3/4 = 1, which is not possible given the initial conditions. There must be an additional piece of information, perhaps involving the length of FH or the value of θ directly. A correctly posed problem would provide enough information to solve for x.
Scenario 6: Coordinate Geometry
If the vertices of the square are represented by coordinates, we can leverage distance formulas and properties of slopes to find x.
Problem: The vertices of square FGHI are F(0,0), G(4x, 0), H(4x, 4x), and I(0, 4x). If the area of the square is 100 square units, find x.
Solution:
The side length of the square is the distance between two adjacent vertices, such as F and G:
Distance FG = √[(4x - 0)² + (0 - 0)²] = 4x
Area = (side length)² = (4x)² = 16x²
Given that the area is 100:
16x² = 100
x² = 100/16 = 25/4
x = ±5/2
Since length cannot be negative, x = 5/2.
Advanced Scenarios and Problem-Solving Techniques
More complex problems might involve:
- Inscribed or Circumscribed Circles: Problems might involve the radius of a circle inscribed within or circumscribed around the square.
- Combination of Shapes: The square might be part of a larger composite shape, requiring a more nuanced approach.
- Systems of Equations: Multiple equations might be needed to solve for x simultaneously.
For these advanced problems, it's important to:
- Draw a Diagram: Visualizing the problem is crucial.
- Identify Relevant Properties: Pinpoint the relevant properties of squares and other shapes involved.
- Write Down Equations: Translate the geometrical relationships into algebraic equations.
- Solve the Equations: Utilize algebraic techniques to solve for x.
- Check Your Answer: Verify your solution by substituting the value of x back into the original problem.
Conclusion
Solving for 'x' within the context of a square involves a systematic approach that combines a strong understanding of the square's properties with algebraic problem-solving skills. By working through various scenarios and employing different techniques, we can enhance our geometrical reasoning abilities and build confidence in tackling complex geometrical problems. Remember to always visualize the problem, identify relevant properties, write down equations, and carefully check your answer. This methodical approach will unlock the solutions to even the most challenging square-based equations.
Latest Posts
Latest Posts
-
Express Cos D As A Fraction In Simplest Terms
Jun 04, 2025
-
Which Expression Is Equivalent To 8x 12y 32
Jun 04, 2025
-
Peer Pressure Can Influence All Of The Following Except
Jun 04, 2025
-
How Might A Psychiatrist Describe A Paper Plate
Jun 04, 2025
-
No Tengo Nada En Mi Bolsillo Scarf Pocket Sunglasses Style
Jun 04, 2025
Related Post
Thank you for visiting our website which covers about If Fghi Is A Square Solve For X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.