Solve A 2x 6xz For X
Breaking News Today
Jun 05, 2025 · 5 min read
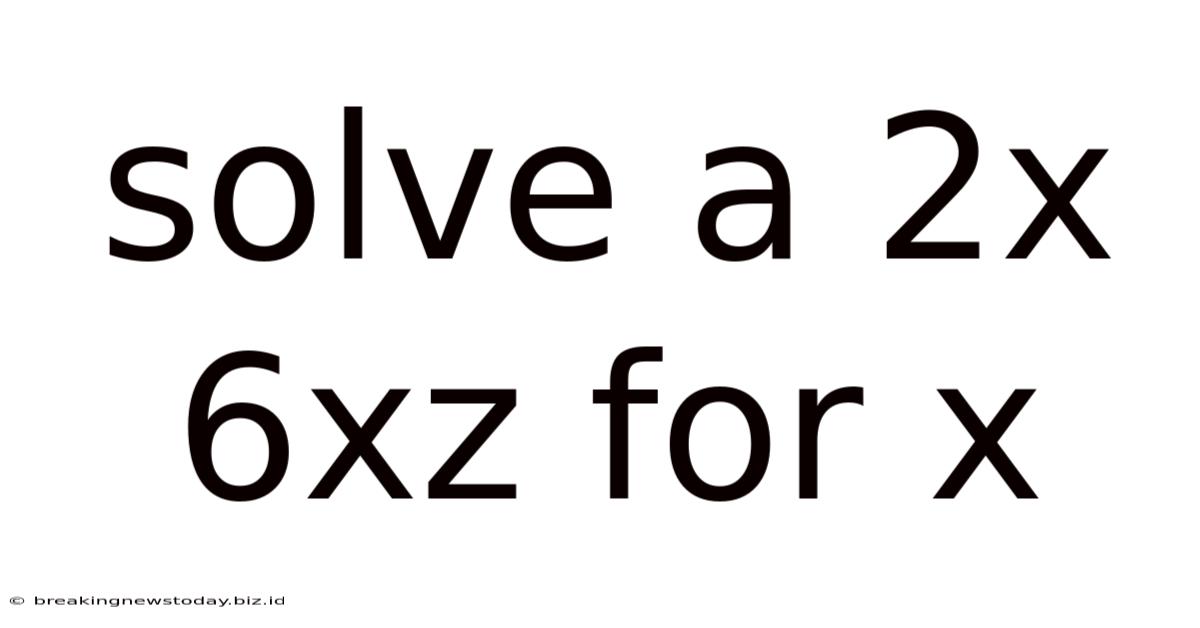
Table of Contents
Solving for x: A Comprehensive Guide to 2x + 6xz = 0
This article provides a detailed walkthrough on how to solve the equation 2x + 6xz = 0 for the variable x. We'll explore various methods, discuss the underlying mathematical principles, and examine potential scenarios and interpretations. This isn't just about finding a single solution; it's about understanding the process, its implications, and its broader applications in algebra and beyond.
Understanding the Equation:
The equation 2x + 6xz = 0 is a linear equation in two variables, x and z. The goal is to isolate 'x' on one side of the equation, expressing it in terms of 'z' (or demonstrating that 'x' has specific values regardless of 'z'). This type of problem frequently appears in algebra, calculus, and various applied mathematical fields. Mastering this fundamental skill is crucial for more advanced mathematical concepts.
Method 1: Factoring and the Zero Product Property
This is arguably the most efficient method for solving this particular equation. The core principle lies in the Zero Product Property, which states that if the product of two or more factors is zero, then at least one of the factors must be zero.
-
Factor out the common term: Notice that both terms, 2x and 6xz, share a common factor of '2x'. We can factor this out:
2x(1 + 3z) = 0
-
Apply the Zero Product Property: Since the product of 2x and (1 + 3z) equals zero, either 2x = 0 or (1 + 3z) = 0.
-
Solve for x in each case:
-
Case 1: 2x = 0 Dividing both sides by 2 gives us: x = 0
-
Case 2: 1 + 3z = 0 Subtracting 1 from both sides gives: 3z = -1 Dividing both sides by 3 gives: z = -1/3
-
Therefore, the solutions to the equation 2x + 6xz = 0 are x = 0 and z = -1/3. Note that x = 0 is a solution regardless of the value of z. Conversely, z = -1/3 is only a solution when x is not zero.
Method 2: Rearranging and Solving for x
This method involves manipulating the equation algebraically to isolate x.
-
Move the term with x and z to the other side: Subtract 6xz from both sides of the original equation:
2x = -6xz
-
Factor out x: Notice that both terms on the right-hand side now have an x. We can factor this out:
2x = x(-6z)
-
Add 6xz to both sides: This step is a bit trickier than the previous method.
2x + 6xz = 0
-
Factor out x:
x(2 + 6z) = 0
-
Apply the Zero Product Property:
- x = 0
- 2 + 6z = 0 => 6z = -2 => z = -1/3
This method arrives at the same solutions as the factoring method: x = 0 and z = -1/3.
Method 3: Considering Different Scenarios
Let's analyze the equation's behavior under different conditions.
-
If z = 0: The equation simplifies to 2x = 0, leading directly to x = 0.
-
If x = 0: The equation becomes 0 = 0, which is always true, regardless of the value of z. This confirms that x = 0 is a solution for any value of z.
-
If x ≠ 0: We can divide the original equation by x:
2 + 6z = 0
Solving for z gives:
z = -1/3
This approach highlights that if x is not zero, then z must be -1/3 to satisfy the equation. This reinforces the solutions obtained through the previous methods.
Interpreting the Solutions:
The solutions x = 0 and z = -1/3 represent specific points or lines in a coordinate system where x and z are the axes. The solution x = 0 represents a line along the z-axis (where x is always zero). The solution z = -1/3 represents a line parallel to the x-axis where z is always -1/3. The intersection of these lines reflects the simultaneous solution for both variables.
Expanding the Understanding: Beyond Simple Linear Equations
The techniques used to solve 2x + 6xz = 0 are fundamental building blocks for solving more complex equations. These techniques can be extended to:
-
Quadratic Equations: Equations involving x² terms often require factoring, the quadratic formula, or completing the square. The ability to factor, as demonstrated above, is crucial for these types of problems.
-
Systems of Equations: Problems involving multiple equations with multiple variables necessitate techniques like substitution or elimination to find solutions.
-
Polynomial Equations: Higher-order polynomials (x³, x⁴, etc.) require more advanced methods, but the principles of factoring and the zero product property remain crucial.
-
Nonlinear Equations: Equations containing exponential, logarithmic, or trigonometric functions often require more specialized techniques, but understanding basic algebraic manipulation remains essential.
Practical Applications:
Understanding how to solve equations like 2x + 6xz = 0 is not just an academic exercise. This type of problem appears in numerous real-world applications, including:
-
Physics: Solving for variables in equations describing motion, forces, or energy.
-
Engineering: Determining unknown parameters in designs or calculations.
-
Economics: Modeling relationships between variables in economic models.
-
Computer Science: Solving algorithms and developing programs.
Conclusion:
Solving the equation 2x + 6xz = 0 for x, using factoring or algebraic rearrangement, reveals two solutions: x = 0 (for any z) and z = -1/3 (when x ≠ 0). Understanding these methods is essential not only for succeeding in algebra but also for applying mathematical reasoning to a wide range of practical problems. The principles illustrated here—factoring, applying the zero product property, and strategic algebraic manipulation—form the foundation for tackling far more complex equations in the future. Mastering these fundamental techniques builds a strong mathematical foundation for more advanced concepts and applications. The ability to solve for x efficiently and accurately is a valuable skill across various disciplines.
Latest Posts
Latest Posts
-
12 Is What Percent Of 144
Jun 06, 2025
-
Humans Are Classified As Omnivores Phrase Or Clause
Jun 06, 2025
-
In The Following Conversation Which Group Discussion Technique
Jun 06, 2025
-
Part Of The Process For Evaluating A Video Is
Jun 06, 2025
-
In The Url Http Www Simnetonline Com What Is The Domain Name
Jun 06, 2025
Related Post
Thank you for visiting our website which covers about Solve A 2x 6xz For X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.