Solve Y 4x Rx 6 For X
Breaking News Today
Jun 05, 2025 · 6 min read
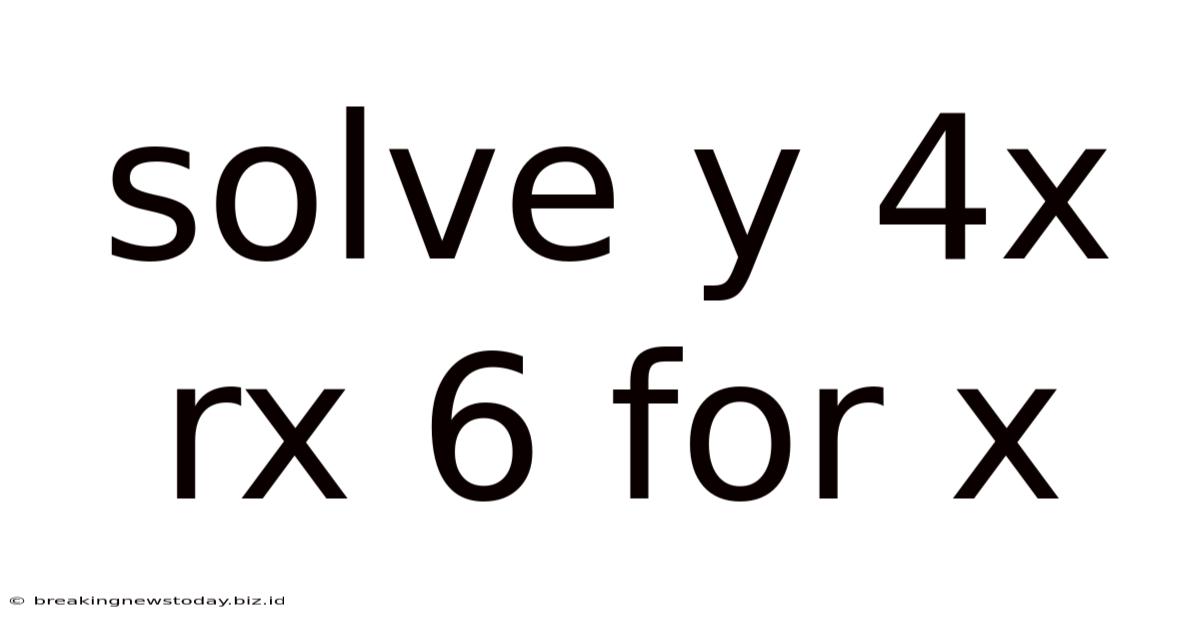
Table of Contents
Solving for x: A Comprehensive Guide to y = 4x + rx + 6
Solving algebraic equations is a fundamental skill in mathematics, crucial for various applications in science, engineering, and everyday life. This article provides a comprehensive guide on how to solve the equation y = 4x + rx + 6 for the variable 'x'. We'll explore different approaches, emphasizing the underlying principles and offering practical tips to enhance your understanding and problem-solving skills. We'll also delve into the importance of understanding the context of such equations and how they appear in real-world scenarios.
Understanding the Equation: y = 4x + rx + 6
Before diving into the solution, let's analyze the equation itself. y = 4x + rx + 6 is a linear equation in two variables, 'x' and 'y'. The presence of 'r' adds a layer of complexity, as 'r' can represent a constant value or a parameter that changes depending on the specific context of the problem. This means the solution for 'x' will depend on the value of 'r' and 'y'.
The equation is a linear equation because the highest power of 'x' is 1. This means the graph of this equation will be a straight line. The terms '4x' and 'rx' are terms that involve the variable x and represent different contributions to the overall value of y. The constant term '6' represents the y-intercept (the point where the line crosses the y-axis).
Method 1: Factoring and Solving
The most straightforward method to solve for 'x' involves factoring and applying basic algebraic manipulation.
1. Combine like terms:
The first step is to combine the terms involving 'x':
y = (4 + r)x + 6
2. Isolate the term with 'x':
To isolate the term containing 'x', subtract 6 from both sides of the equation:
y - 6 = (4 + r)x
3. Solve for 'x':
Finally, to solve for 'x', divide both sides of the equation by (4 + r):
x = (y - 6) / (4 + r)
Important Consideration: This solution is valid only if (4 + r) ≠ 0. If (4 + r) = 0, then the equation becomes y - 6 = 0, implying that y = 6. In this specific case, the value of 'x' would be indeterminate because any value of 'x' satisfies the equation.
Method 2: Using the Quadratic Formula (if applicable)
While the given equation is linear in x, some variations might lead to a quadratic equation. Let's explore a hypothetical scenario.
Suppose the equation was slightly different: y = 4x² + rx + 6. This equation is now quadratic in x because the highest power of x is 2. Solving for x in this case requires a different approach: the quadratic formula.
The standard form of a quadratic equation is ax² + bx + c = 0. In our hypothetical case:
- a = 4
- b = r
- c = -y + 6
The quadratic formula is:
x = (-b ± √(b² - 4ac)) / 2a
Substituting our values, we get:
x = (-r ± √(r² - 4 * 4 * (-y + 6))) / (2 * 4)
x = (-r ± √(r² + 16y - 96)) / 8
This provides two possible solutions for 'x', denoted by the ± symbol. The discriminant (b² - 4ac = r² + 16y - 96) determines the nature of the solutions. If the discriminant is positive, there are two distinct real solutions. If it's zero, there's one real solution. If it's negative, there are no real solutions (only complex solutions).
Interpreting the Solution and its Implications
The solution x = (y - 6) / (4 + r) reveals a crucial relationship between x, y, and r. It highlights that x is a function of both y and r.
-
Dependence on y: As y increases, x also increases (assuming 4 + r > 0). This direct relationship signifies that 'y' influences 'x' proportionally.
-
Dependence on r: The value of 'r' significantly affects the solution. A larger 'r' value (assuming r > -4) results in a smaller value of x, and vice versa. The behavior is inversely proportional when the denominator is positive. This sensitivity to 'r' underscores the importance of understanding the context in which 'r' is defined and its implications for 'x'.
-
The role of the constant term: The constant term '6' represents the vertical shift of the line. Changing this constant would affect the y-intercept, leading to a change in 'x' for the same value of 'y' and 'r'.
Real-World Applications and Examples
Linear equations like y = 4x + rx + 6 appear frequently in various real-world situations:
-
Modeling financial growth: 'x' could represent time (in years), 'y' could be the total amount of money in an account, '4' could be a fixed annual interest, 'r' could be a variable interest rate dependent on market conditions, and '6' could be an initial deposit. Solving for 'x' would help determine the time it takes to reach a certain amount of money.
-
Analyzing scientific data: In scientific experiments, 'x' might be an independent variable (e.g., temperature), 'y' the dependent variable (e.g., reaction rate), '4' and 'r' might be constants derived from experimental data, and '6' a baseline value. Solving for x could help determine the temperature required for a specific reaction rate.
-
Predictive modeling: Linear equations can be used to build models for various predictions. Understanding how changes in one variable (x) affect another (y) is crucial for making predictions.
-
Engineering and Physics: Linear equations are fundamental to many principles in engineering and physics. They represent relationships between physical quantities.
Beyond the Basics: Dealing with Complex Scenarios
Let's consider some more complex scenarios that might arise:
-
Systems of Equations: The equation
y = 4x + rx + 6could be part of a system of equations. Solving such a system would involve solving multiple equations simultaneously to find the values of 'x' and 'y' (and possibly other variables) that satisfy all the equations. Methods like substitution, elimination, or matrix methods could be employed. -
Non-linear Extensions: As discussed earlier, a slight change in the equation could lead to a quadratic or higher-order polynomial equation, requiring more advanced techniques to solve.
-
Equations with constraints: The problem might involve constraints or conditions on the values of x, y, and r. For example, x might be limited to positive values, or r might be restricted to a certain range. These constraints will need to be considered while finding the solution.
-
Numerical Methods: For complex equations or systems that are difficult to solve analytically, numerical methods could be employed to obtain approximate solutions. These techniques involve iterative calculations to approach the solution gradually.
Conclusion: Mastering Algebraic Problem Solving
Solving the equation y = 4x + rx + 6 for 'x' is a foundational exercise that demonstrates the importance of mastering algebraic manipulation. By understanding the different methods involved, considering various scenarios, and interpreting the results within a real-world context, you can build a strong foundation for tackling more complex mathematical problems. Remember that mathematical proficiency isn't just about memorizing formulas; it's about understanding the underlying principles and applying those principles creatively to solve a wide variety of problems. Practice is key, and exploring diverse examples will significantly enhance your algebraic skills. The ability to solve equations like this forms a crucial part of your mathematical toolkit and will benefit you in various academic and professional pursuits.
Latest Posts
Latest Posts
-
Berry Gordys Desire To Appeal To White Audiences Prompted
Jun 06, 2025
-
What Is The Gcf Of 96x5 And 64x2
Jun 06, 2025
-
Which Of The Following Statements Is True Of Aquatic Biomes
Jun 06, 2025
-
Bob Can Do A Job In 5 Hours
Jun 06, 2025
-
Hemingway Uses Vague Pronouns And Simple Language To
Jun 06, 2025
Related Post
Thank you for visiting our website which covers about Solve Y 4x Rx 6 For X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.