Two Times The Sum Of Number And 5 Is 20
Breaking News Today
Jun 01, 2025 · 4 min read
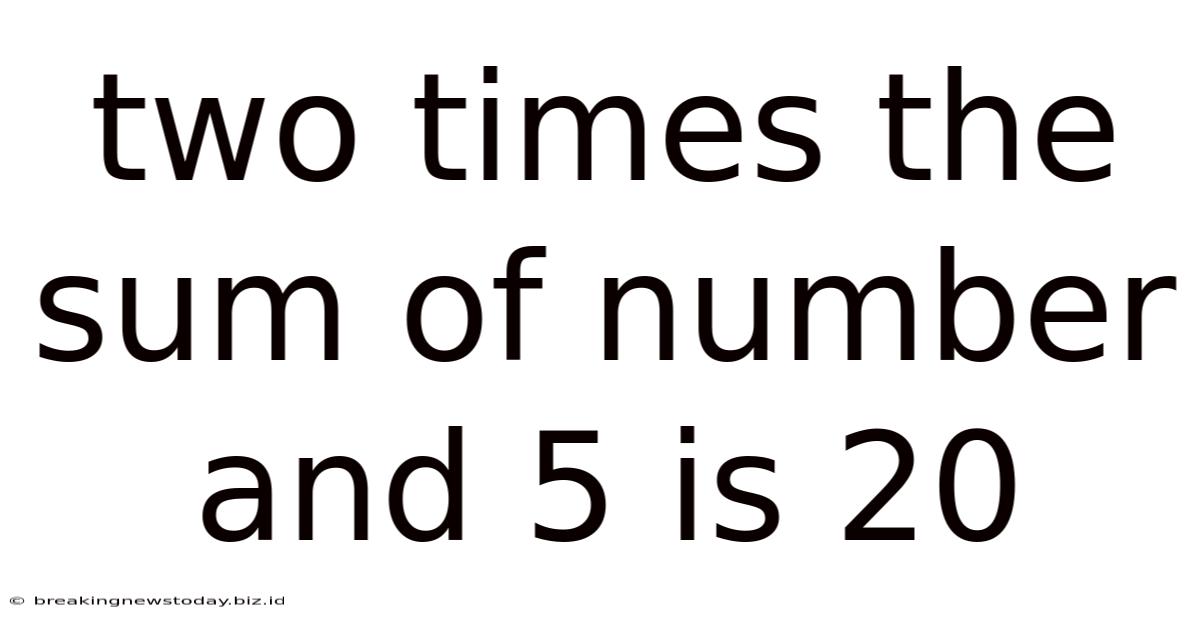
Table of Contents
Two Times the Sum of a Number and 5 is 20: Unraveling the Mathematical Mystery
This seemingly simple mathematical statement, "Two times the sum of a number and 5 is 20," hides a wealth of concepts relevant to algebra, problem-solving, and even real-world applications. Let's delve into this seemingly simple equation and explore its various facets, from solving for the unknown number to understanding the broader mathematical principles involved.
Deconstructing the Problem: From Words to Equation
The beauty of mathematics lies in its ability to translate real-world problems into concise, solvable equations. The statement "Two times the sum of a number and 5 is 20" needs to be transformed from a verbal description into a mathematical expression. Let's break it down step-by-step:
- A number: We'll represent this unknown number with a variable, typically 'x'.
- The sum of a number and 5: This translates to x + 5.
- Two times the sum of a number and 5: This becomes 2(x + 5). Notice the use of parentheses to indicate that the multiplication applies to the entire sum.
- is 20: This signifies equality, giving us the complete equation: 2(x + 5) = 20.
Solving the Equation: Unveiling the Mystery Number
Now that we have our equation, 2(x + 5) = 20, we can employ algebraic techniques to solve for 'x'. There are several approaches, and we'll explore a couple:
Method 1: Distributive Property
The distributive property states that a(b + c) = ab + ac. Applying this to our equation:
- Distribute the 2: 2 * x + 2 * 5 = 20, simplifying to 2x + 10 = 20.
- Subtract 10 from both sides: 2x + 10 - 10 = 20 - 10, resulting in 2x = 10.
- Divide both sides by 2: 2x / 2 = 10 / 2, giving us the solution: x = 5.
Therefore, the number is 5.
Method 2: Divide First, then Solve
Alternatively, we can simplify the equation by dividing both sides by 2 before applying the distributive property:
- Divide both sides by 2: 2(x + 5) / 2 = 20 / 2, which simplifies to x + 5 = 10.
- Subtract 5 from both sides: x + 5 - 5 = 10 - 5, resulting in x = 5.
This method demonstrates that there's often more than one correct path to a solution in mathematics. Choosing the most efficient method often depends on the specific equation and individual preference.
Verifying the Solution: Checking Your Work
It's crucial to verify your solution by substituting the value of 'x' back into the original equation:
2(x + 5) = 20
2(5 + 5) = 20
2(10) = 20
20 = 20
Since the equation holds true, our solution, x = 5, is correct.
Expanding the Concept: Similar Problems and Applications
The core concept of translating word problems into algebraic equations is fundamental to many mathematical applications. Let's explore some similar problems and real-world scenarios where this skill is invaluable:
Example 1: Slightly More Complex Problem
"Three times the difference between a number and 2 is 18."
This problem can be expressed as: 3(x - 2) = 18. Solving this using similar methods as above will yield the solution x = 8.
Example 2: Real-World Application – Geometry
Imagine calculating the perimeter of a rectangle. If the length is 5 more than the width, and the perimeter is 20, the equation would be: 2(x + x + 5) = 20, where 'x' represents the width. Solving this will allow you to find both the length and the width of the rectangle.
Example 3: Financial Calculations
Consider a scenario where you invest a certain amount of money, and the investment doubles plus an additional $10, resulting in $30. The equation would be: 2x + 10 = 30, where 'x' represents your initial investment. Solving for x will show how much money you initially invested.
Beyond the Basics: Developing Mathematical Proficiency
This simple equation acts as a gateway to more complex mathematical concepts. Mastering the process of translating word problems into equations and solving them builds a strong foundation for:
- Advanced Algebra: This includes solving more complex equations with multiple variables and inequalities.
- Calculus: Understanding the relationship between variables is crucial in calculus, where we analyze rates of change and functions.
- Real-world problem-solving: The ability to model real-world scenarios using mathematical equations is a valuable skill in various professions, from engineering and finance to science and data analysis.
Practicing Your Skills: Exercises and Further Exploration
To solidify your understanding, try solving the following problems:
- Five times the sum of a number and 3 is 35. Find the number.
- Twice the difference between a number and 7 is 12. Find the number.
- The perimeter of a square is 28 cm. Find the length of one side.
Remember, practice is key to mastering any mathematical concept. Work through various problems, experiment with different solution methods, and don't be afraid to seek help when needed. The more you practice, the more confident and proficient you’ll become in translating word problems into equations and solving them efficiently. Understanding these fundamentals opens doors to a wider appreciation of the power and elegance of mathematics in various aspects of life.
Latest Posts
Latest Posts
-
For Every Pound Of Feed Consumed By The Animal
Jun 03, 2025
-
What Is The Greatest Common Factor Of 4xy2 And 20x2y4
Jun 03, 2025
-
Which Of The Following Is True Of A Research Proposal
Jun 03, 2025
-
How Much Momentum Does A Spaceship Carrying Rocks Have
Jun 03, 2025
-
Which Themes Are Found In The Odyssey Select Three Answers
Jun 03, 2025
Related Post
Thank you for visiting our website which covers about Two Times The Sum Of Number And 5 Is 20 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.