Use A Number Line To Solve 235+123
Breaking News Today
Jun 04, 2025 · 5 min read
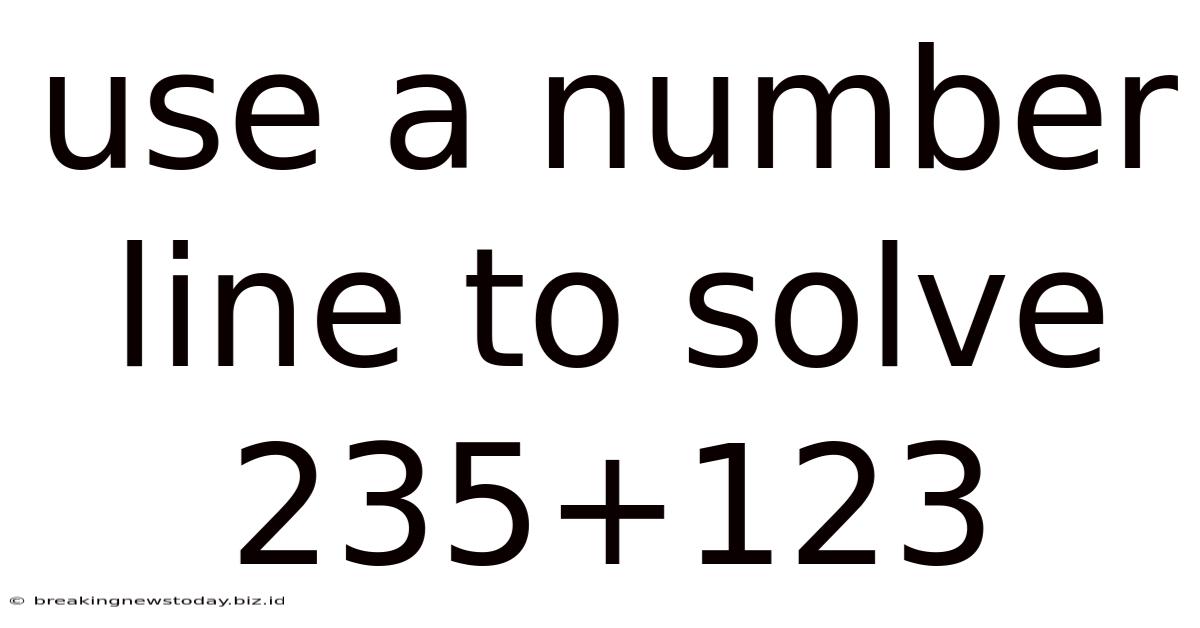
Table of Contents
Using a Number Line to Solve 235 + 123: A Comprehensive Guide
Adding numbers might seem simple, especially with smaller digits. However, understanding the underlying mathematical concepts is crucial for building a strong foundation in arithmetic. This article will delve deep into using a number line to solve the addition problem 235 + 123, breaking down the process step-by-step and explaining the underlying principles. We'll also explore why this method is valuable, even as you progress to more complex mathematical operations.
What is a Number Line?
A number line is a visual representation of numbers on a straight line. It's a fundamental tool in mathematics, used to illustrate various concepts including addition, subtraction, multiplication, and division. The line extends infinitely in both directions, typically marked with equally spaced points representing integers (whole numbers). Zero (0) is usually placed in the center, with positive numbers extending to the right and negative numbers extending to the left.
Key Features of a Number Line:
- Origin (Zero): The starting point, representing the number 0.
- Positive Numbers: Numbers greater than 0, located to the right of 0.
- Negative Numbers: Numbers less than 0, located to the left of 0.
- Equal Intervals: The distance between consecutive numbers is consistent.
Solving 235 + 123 Using a Number Line: A Step-by-Step Approach
While calculators provide quick answers, using a number line allows you to visualize the addition process, enhancing your understanding. Let's solve 235 + 123 step-by-step using the number line method:
Step 1: Representing the First Number
Begin by locating the first number, 235, on the number line. Since we're dealing with relatively large numbers, you might not be able to mark every single integer. Instead, focus on marking key intervals or significant points to make the visualization manageable. You can even use a scale, such as marking every 50 or 100 units.
Step 2: Adding the Hundreds Digit
The number 123 has one hundred (100). From your marked 235 on the number line, move 100 units to the right. This will land you at 335. This visually represents adding the hundreds place value of 123.
Step 3: Adding the Tens Digit
Next, we need to add the tens digit from 123, which is 20. From your current position (335), move 20 units to the right. This brings you to 355. This visualizes the addition of the tens place value.
Step 4: Adding the Units Digit
Finally, add the units digit from 123, which is 3. From 355, move 3 units to the right. This will lead you to 358. This completes the addition of the ones place value.
Step 5: The Final Result
The point you reach after adding all the place values (358) is the final answer to the equation 235 + 123. Therefore, 235 + 123 = 358.
Visualizing the Process: A Detailed Example
Let's create a more detailed illustration, although drawing a full number line with each integer from 0 to 358 isn't practical. We'll focus on key markers to illustrate the process:
0 50 100 150 200 250 300 350 400
|-------|-------|-------|-------|-------|-------|-------|-------|
Start at 235 (approximately here)
---> +100 (move to the right by 100) ---> 335
---> +20 (move to the right by 20) ---> 355
---> +3 (move to the right by 3) ---> 358
This simplified representation clearly shows the stepwise addition using the number line.
Why Use a Number Line for Addition?
While seemingly elementary for simple additions, the number line method offers significant advantages:
- Visual Understanding: It provides a concrete visual representation of the addition process, making it easier for beginners to grasp the concept of adding numbers. This is particularly useful for students who learn best through visual aids.
- Reinforces Place Value: The process highlights the importance of place value (hundreds, tens, and ones) in addition. Moving in increments of 100, 10, and 1 reinforces this fundamental mathematical concept.
- Foundation for More Complex Operations: The number line is not just limited to addition. It lays the foundation for understanding subtraction, multiplication, and even division. The visual representation of movement along the line forms a basis for comprehending these more advanced operations.
- Improved Number Sense: Regular use of the number line helps develop stronger number sense – a crucial skill in mathematics. It allows for a better understanding of the magnitude and relationship between different numbers.
- Problem Solving: The visual approach enhances problem-solving skills. Students learn to break down complex problems into smaller, manageable steps, a valuable technique applicable to various mathematical and real-world scenarios.
Extending the Concept: Larger Numbers and Different Operations
The number line method can be applied to larger numbers and different mathematical operations. For very large numbers, you might need to use a scale, for example, representing every 1000 units instead of every single unit.
Subtraction: Subtraction is also easily represented using a number line. Instead of moving to the right (adding), you move to the left (subtracting).
Multiplication: Multiplication can be visualized as repeated addition. For instance, 3 x 4 can be represented by starting at 0 and moving 4 units to the right three times.
Division: Division can be shown as repeated subtraction. For example, 12 ÷ 3 can be visualized by starting at 12 and repeatedly subtracting 3 until you reach 0; the number of times you subtract represents the answer.
Incorporating Number Lines into Teaching and Learning
Incorporating number lines into the teaching and learning process offers numerous benefits:
- Interactive Learning: Number lines can be used to create interactive activities and games that make learning more engaging.
- Concrete Examples: They provide concrete examples of abstract mathematical concepts, making it easier for students to understand and retain information.
- Differentiated Instruction: The number line method can be adapted to suit different learning styles and abilities.
- Assessment: Teachers can use number lines to assess students' understanding of addition and other mathematical operations.
Conclusion: The Enduring Value of the Number Line
The number line, while seemingly a simple tool, plays a vital role in building a strong mathematical foundation. By using it to solve even simple equations like 235 + 123, we not only get the correct answer (358) but also deepen our understanding of fundamental mathematical principles. This visual method enhances number sense, problem-solving skills, and provides a valuable stepping stone towards mastering more complex mathematical concepts. Its versatility and adaptability make it an invaluable teaching aid and learning tool for students of all ages and abilities. The enduring value of the number line lies in its ability to make abstract mathematical concepts concrete and accessible.
Latest Posts
Latest Posts
-
Select All The Individuals Who Were Notable Students Of Schoenberg
Jun 06, 2025
-
Suppose You Re Studying The Forms Of City Government
Jun 06, 2025
-
What Is The Value Of The 0 In 302
Jun 06, 2025
-
Which Fraction Has The Same Value As 55 5
Jun 06, 2025
-
Which Vision Is First Affected By Fatigue Drugs And Speed
Jun 06, 2025
Related Post
Thank you for visiting our website which covers about Use A Number Line To Solve 235+123 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.