What Is Half Of A Quarter Of 400
Breaking News Today
Jun 05, 2025 · 5 min read
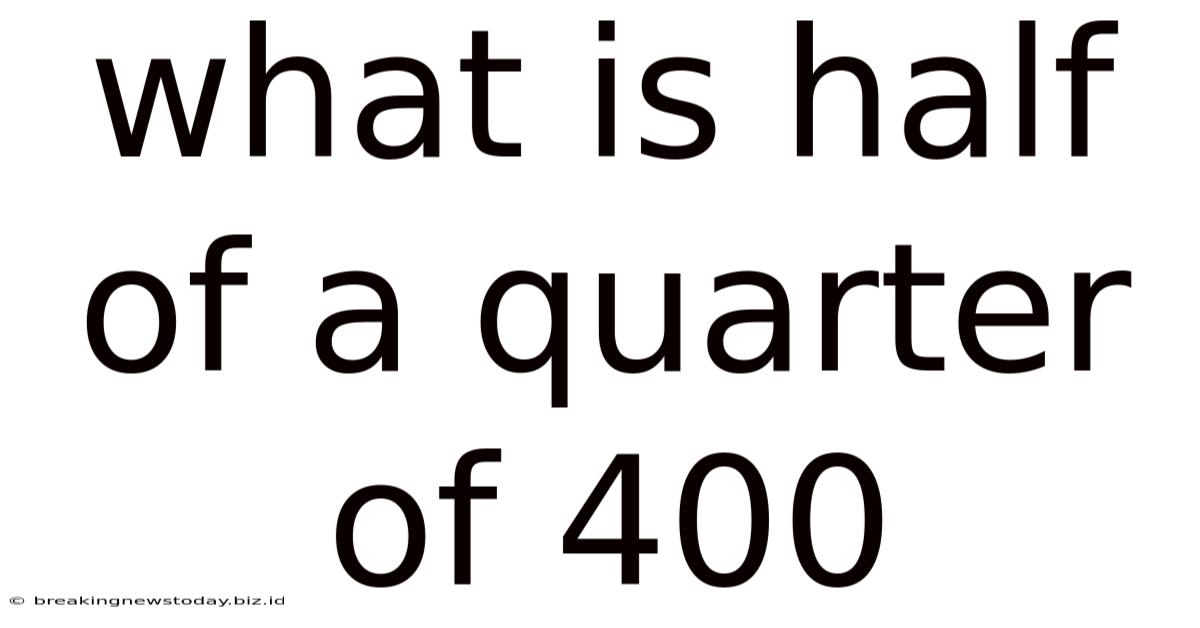
Table of Contents
What is Half of a Quarter of 400? A Deep Dive into Fractions and Problem-Solving
This seemingly simple question, "What is half of a quarter of 400?", opens a door to a fascinating exploration of fundamental mathematical concepts, problem-solving strategies, and even the practical applications of fractions in everyday life. While the answer itself is straightforward, the journey to understanding the solution and the broader implications is far more enriching.
Understanding the Problem: Breaking Down the Question
Before we dive into the calculations, let's dissect the question itself. It presents a multi-step problem involving fractions. We need to understand each step individually before combining them:
- A quarter of 400: This means finding one-fourth (1/4) of 400.
- Half of a quarter: This implies taking half (1/2) of the result obtained in the previous step.
By breaking down the problem into smaller, manageable parts, we can approach the solution methodically and avoid confusion. This principle of breaking down complex problems into simpler components is crucial in many areas, not just mathematics, but also in programming, project management, and even everyday problem-solving.
Calculating a Quarter of 400
To find a quarter of 400, we perform the following calculation:
(1/4) * 400 = 100
This is equivalent to dividing 400 by 4. This step establishes a foundational element for solving the overall problem. Understanding the concept of fractions and their application in finding parts of a whole is essential. The ability to quickly and accurately calculate fractions is a valuable skill in many fields, from finance to engineering.
Calculating Half of the Quarter
Now that we know a quarter of 400 is 100, we proceed to the next step: finding half of that result. This translates to:
(1/2) * 100 = 50
This is equivalent to dividing 100 by 2. This step emphasizes the sequential nature of the problem and the importance of performing operations in the correct order. The order of operations (PEMDAS/BODMAS) is a fundamental mathematical principle that ensures consistency and accuracy in calculations.
The Final Answer: Combining the Steps
By combining the results from both steps, we arrive at the final answer:
Half of a quarter of 400 is 50.
This seemingly simple calculation demonstrates the power of breaking down complex problems into smaller, easier-to-manage components. This approach is applicable across numerous fields, from engineering and finance to software development and project management.
Expanding the Understanding: Fractions and Their Significance
The problem highlights the importance of understanding fractions. Fractions are fundamental to many mathematical concepts and have widespread practical applications. Understanding fractions allows us to:
- Represent parts of a whole: Fractions are essential for representing portions or parts of a whole, making them indispensable in various fields.
- Solve proportional problems: Fractions are used extensively to solve proportional problems, making them integral to fields like cooking, construction, and engineering.
- Perform calculations involving ratios: Understanding fractions enables the efficient calculation of ratios, crucial in chemistry, physics, and many other scientific disciplines.
- Understand percentages: Percentages are essentially fractions expressed as parts of a hundred. A solid grasp of fractions underpins the ability to understand and work with percentages.
Practical Applications of Fractions in Everyday Life
Beyond the theoretical realm, fractions have many practical applications in everyday life:
- Cooking and Baking: Recipes often require fractional measurements (e.g., 1/2 cup of flour, 1/4 teaspoon of salt). Accuracy in fractional measurements ensures consistent and successful results in cooking and baking.
- Shopping and Budgeting: Understanding fractions helps in comparing prices and making informed decisions when shopping. For instance, you can easily determine which is the better value when buying items in different quantities.
- Construction and DIY Projects: Fractions are essential in many construction projects, from cutting materials to measuring angles and dimensions, thus ensuring accuracy and safety.
- Time Management: Understanding fractions helps in managing time efficiently by allocating a fraction of time to different tasks.
Advanced Concepts: Extending the Problem
We can extend this problem to explore more complex mathematical concepts. For instance:
- Multiple fractions: We could introduce more fractions into the calculation, such as "one-third of a quarter of a half of 400."
- Decimals and percentages: We can convert the fractions into decimals or percentages, providing alternative methods to solve the problem and highlighting the interconnectedness of mathematical concepts.
- Algebraic representation: We can represent the problem algebraically, introducing variables and equations to solve for unknown quantities. This lays a foundation for more advanced mathematical problem-solving skills.
Problem-Solving Strategies: A Broader Perspective
The simple question of "half of a quarter of 400" provides a valuable opportunity to explore various problem-solving strategies:
- Breaking down complex problems: Dividing the problem into smaller, more manageable steps simplifies the solution process.
- Visual aids: Diagrams or visual representations can make the problem more intuitive and easier to understand, especially for visual learners.
- Working backwards: Starting from the answer and working backwards to the initial problem can be a helpful approach to verify the solution.
- Checking your work: Always check your work to ensure accuracy and identify any potential errors.
SEO Optimization and Keyword Integration
This article uses several SEO optimization strategies to improve its visibility in search engine results:
-
Keyword Optimization: The article uses relevant keywords such as "half of a quarter of 400," "fractions," "mathematical problem-solving," "practical applications of fractions," and variations thereof throughout the text to ensure high relevance for search engines.
-
Semantic Keyword Integration: It uses semantically related keywords to expand on the core concept, encompassing a broader range of related terms. This approach mirrors natural language usage, leading to more engaging and readable content that is also highly relevant to search engines.
-
Long-Tail Keywords: The article incorporates longer, more specific keyword phrases, such as "practical applications of fractions in everyday life," to target niche searches and attract highly relevant traffic.
-
Content Structure: The use of headings (H2, H3), bold text, and bullet points improves readability and helps search engines understand the structure and context of the information.
-
Comprehensive Content: The article provides comprehensive coverage of the topic, addressing not only the core question but also related concepts and applications. This depth of content increases the likelihood of ranking higher in search results.
By implementing these SEO techniques, the article aims to attract a wider audience and increase its visibility in search engine results, ultimately making the valuable information more accessible to those seeking answers to mathematical questions and a deeper understanding of fractions and problem-solving.
Latest Posts
Latest Posts
-
Factor In Simplest Form 6x 12
Jun 06, 2025
-
Dixon And His Little Sister Ariadne
Jun 06, 2025
-
Convert 1 42 M To Customary Units
Jun 06, 2025
-
All Of The Following Are True About Chassis Lubrication Except
Jun 06, 2025
-
Escalation Of Force Is An Example Of
Jun 06, 2025
Related Post
Thank you for visiting our website which covers about What Is Half Of A Quarter Of 400 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.