Which Line Is Parallel To The Line 8x 2y 12
Breaking News Today
Jun 04, 2025 · 5 min read
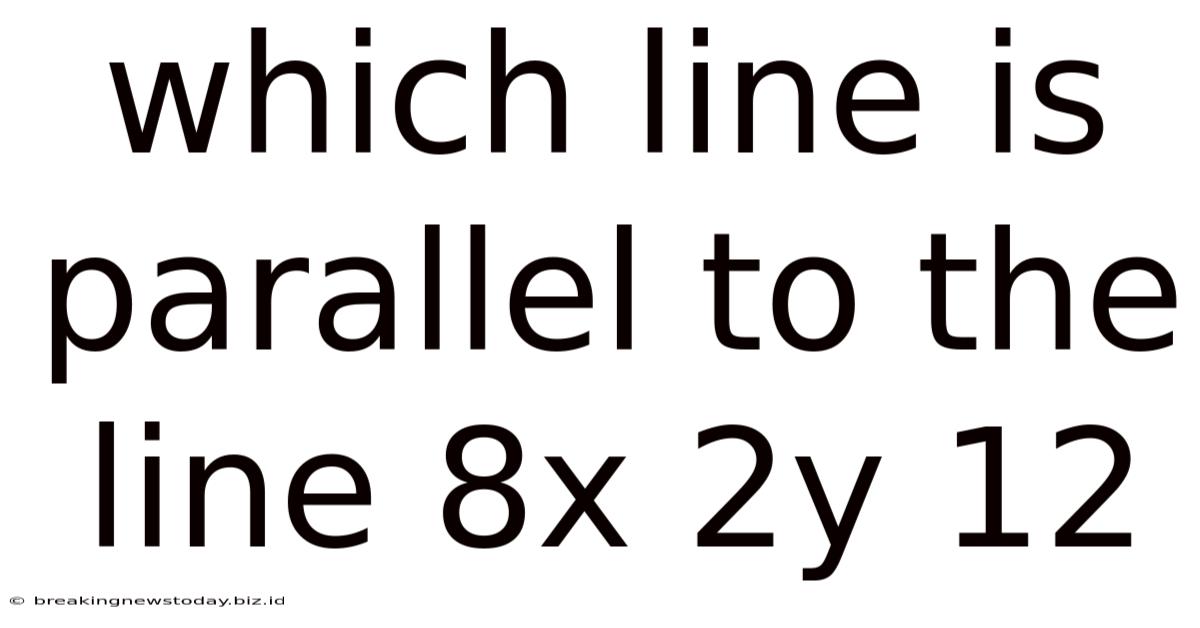
Table of Contents
Which Line is Parallel to the Line 8x + 2y = 12? A Comprehensive Guide
Understanding parallel lines is fundamental in algebra and geometry. This article will delve deep into determining which lines are parallel to the line represented by the equation 8x + 2y = 12, providing a comprehensive explanation suitable for students and anyone looking to refresh their knowledge of linear equations and parallel lines. We'll explore the concept of slope, the relationship between parallel lines and their slopes, and different methods for identifying parallel lines. We will also address common pitfalls and offer practical examples to solidify your understanding.
Understanding the Slope-Intercept Form
Before we determine which lines are parallel to 8x + 2y = 12, let's review the slope-intercept form of a linear equation: y = mx + b.
-
m represents the slope of the line. The slope indicates the steepness and direction of the line. A positive slope indicates an upward slant from left to right, while a negative slope indicates a downward slant. A slope of zero represents a horizontal line, and an undefined slope represents a vertical line.
-
b represents the y-intercept, which is the point where the line crosses the y-axis (where x = 0).
Finding the Slope of 8x + 2y = 12
To find lines parallel to 8x + 2y = 12, we first need to determine the slope of this line. We'll convert the given equation into the slope-intercept form (y = mx + b):
-
Subtract 8x from both sides: 2y = -8x + 12
-
Divide both sides by 2: y = -4x + 6
Now, we can clearly see that the slope (m) of the line 8x + 2y = 12 is -4.
The Key to Parallel Lines: Equal Slopes
The fundamental rule for parallel lines is that they have equal slopes. Parallel lines never intersect; they maintain a constant distance from each other. This constant distance is a direct consequence of their identical slopes. If two lines have different slopes, they will eventually intersect.
Therefore, any line that is parallel to 8x + 2y = 12 will also have a slope of -4.
Identifying Parallel Lines: Examples
Let's analyze several examples to illustrate how to identify lines parallel to 8x + 2y = 12:
Example 1: y = -4x + 10
This equation is already in slope-intercept form. We can immediately see that its slope (m) is -4. Since this slope matches the slope of 8x + 2y = 12, the line y = -4x + 10 is parallel to 8x + 2y = 12. Note that the y-intercept is different; this is perfectly acceptable for parallel lines.
Example 2: 4x + y = 7
Let's convert this equation to slope-intercept form:
- Subtract 4x from both sides: y = -4x + 7
Again, the slope is -4. Therefore, the line 4x + y = 7 is parallel to 8x + 2y = 12.
Example 3: 2y = -8x - 1
Converting to slope-intercept form:
- Divide both sides by 2: y = -4x - 1/2
The slope is -4, confirming that 2y = -8x - 1 is parallel to 8x + 2y = 12.
Example 4: y = -4x
This line also has a slope of -4. Therefore, y = -4x is parallel to 8x + 2y = 12. Note that the y-intercept is 0.
Example 5: x + 4y = 16
Converting to slope-intercept form:
- Subtract x from both sides: 4y = -x + 16
- Divide both sides by 4: y = (-1/4)x + 4
The slope is -1/4, which is not equal to -4. Therefore, this line is not parallel to 8x + 2y = 12.
Example 6: 8x - 2y = 12
Converting to slope-intercept form:
- Subtract 8x from both sides: -2y = -8x + 12
- Divide both sides by -2: y = 4x - 6
The slope is 4, which is not equal to -4. Therefore, this line is not parallel to 8x + 2y = 12. This example highlights that simply having similar numbers in the equation doesn't guarantee parallelism; the slope must be identical.
Beyond the Slope-Intercept Form: Using Other Forms of Linear Equations
While the slope-intercept form is convenient for identifying the slope, you can determine parallelism using other forms of linear equations.
Standard Form (Ax + By = C): Two lines in standard form are parallel if their coefficients of x and y (A and B) are proportional, but their constant terms (C) are different. For example, 8x + 2y = 12 and 4x + y = 5 are parallel because the ratio of the coefficients (8:2 and 4:1) is the same (4:1), but the constant terms differ.
Point-Slope Form (y - y1 = m(x - x1)): Even in point-slope form, the slope (m) remains the key to parallelism. Two lines in point-slope form are parallel if they share the same slope (m) regardless of their points (x1, y1).
Common Pitfalls and Misconceptions
-
Confusing Parallel and Perpendicular Lines: Parallel lines have equal slopes. Perpendicular lines have slopes that are negative reciprocals of each other (e.g., if one slope is m, the other is -1/m). Do not confuse these concepts.
-
Ignoring the Constant Term: The constant term (b in the slope-intercept form, or C in the standard form) affects the y-intercept, but it doesn't influence parallelism. Parallel lines can have different y-intercepts.
-
Incorrectly Converting to Slope-Intercept Form: Always double-check your algebraic steps when converting equations to slope-intercept form. A single error can lead to an incorrect slope and wrong conclusions about parallelism.
Practical Applications of Parallel Lines
The concept of parallel lines has widespread applications in various fields:
-
Engineering and Construction: Parallel lines are essential in designing structures, ensuring stability and accurate measurements.
-
Computer Graphics: Parallel lines are fundamental in creating two-dimensional and three-dimensional images and models.
-
Cartography: Parallel lines are used in map projections and coordinate systems.
-
Physics: Parallel forces and vectors are frequently encountered in mechanics and other branches of physics.
Conclusion
Determining which lines are parallel to a given line involves understanding the concept of slope and the fundamental property that parallel lines possess equal slopes. By converting equations into slope-intercept form or by comparing coefficients in standard form, one can accurately identify parallel lines. Remember to watch out for common pitfalls and always double-check your calculations. Mastering the concept of parallel lines is crucial for success in algebra, geometry, and various practical applications. By understanding the underlying principles and practicing with various examples, you'll build a strong foundation in linear equations and enhance your problem-solving skills.
Latest Posts
Latest Posts
-
35 Of F Is 14 What Is F
Jun 06, 2025
-
Select All The Individuals Who Were Notable Students Of Schoenberg
Jun 06, 2025
-
Suppose You Re Studying The Forms Of City Government
Jun 06, 2025
-
What Is The Value Of The 0 In 302
Jun 06, 2025
-
Which Fraction Has The Same Value As 55 5
Jun 06, 2025
Related Post
Thank you for visiting our website which covers about Which Line Is Parallel To The Line 8x 2y 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.