The Variability Of A Statistic Is Described By
Breaking News Today
Mar 28, 2025 · 6 min read
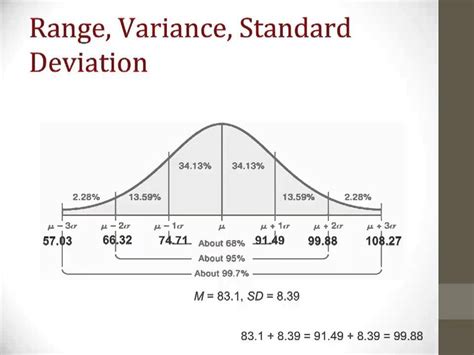
Table of Contents
The Variability of a Statistic: A Deep Dive into Measures of Dispersion
The variability of a statistic is a crucial concept in statistics and data analysis. It describes the spread or dispersion of data points around a central tendency, such as the mean or median. Understanding variability is essential because it helps us assess the reliability and precision of our statistical inferences. A statistic with high variability suggests less precision and more uncertainty in our conclusions, while a statistic with low variability indicates greater reliability and precision. This article explores various aspects of statistical variability, examining the key measures and their applications.
Understanding Statistical Variability
Before delving into specific measures, let's solidify our understanding of what statistical variability represents. It's essentially the extent to which individual data points deviate from the central value. Imagine two datasets representing the heights of students in two different classes. Both classes might have the same average height, but one class might exhibit a much wider range of heights, indicating greater variability. This difference in variability impacts how we interpret the average height. A class with low variability suggests that most students are clustered around the average height, while a class with high variability suggests a broader distribution of heights.
Why is variability important?
Variability is crucial for several reasons:
-
Reliability of inferences: High variability indicates less reliable conclusions based on the data. A highly variable statistic might be heavily influenced by outliers or random fluctuations, leading to inaccurate generalizations.
-
Precision of estimates: Low variability implies more precise estimates of population parameters. When variability is low, our sample statistic provides a more accurate representation of the true population value.
-
Comparison of groups: Variability allows for comparison between different groups or datasets. We can assess whether differences in central tendency are statistically significant by considering the variability within and between groups.
-
Risk assessment: In fields like finance, variability (often represented by measures like standard deviation) is crucial for assessing risk. Higher variability signifies greater uncertainty and potential for extreme outcomes.
Key Measures of Statistical Variability
Several measures quantify statistical variability. The choice of measure depends on the data's characteristics and the research question.
1. Range
The simplest measure of variability is the range, which is the difference between the maximum and minimum values in a dataset. While easy to calculate, the range is highly sensitive to outliers. A single extreme value can drastically inflate the range, making it a less robust measure compared to others.
Example: In a dataset of exam scores: {60, 70, 75, 80, 90, 95, 100}, the range is 100 - 60 = 40.
2. Interquartile Range (IQR)
The interquartile range (IQR) addresses the limitations of the range by focusing on the middle 50% of the data. It is the difference between the third quartile (Q3) – the value separating the upper 25% of data from the lower 75% – and the first quartile (Q1) – the value separating the lower 25% from the upper 75%. The IQR is less sensitive to outliers than the range.
Example: If Q1 = 70 and Q3 = 90, then the IQR is 90 - 70 = 20.
3. Variance
Variance measures the average squared deviation of each data point from the mean. Squaring the deviations ensures that positive and negative deviations don't cancel each other out. The variance is a crucial concept underlying many statistical analyses. However, its units are squared, making it less directly interpretable than some other measures.
The formula for population variance (σ²) is:
σ² = Σ(xᵢ - μ)² / N
where:
- xᵢ represents each data point
- μ represents the population mean
- N represents the population size
For sample variance (s²), the formula is slightly modified:
s² = Σ(xᵢ - x̄)² / (n - 1)
where:
- x̄ represents the sample mean
- n represents the sample size
The denominator (n-1) is used instead of n for sample variance to provide an unbiased estimator of the population variance.
4. Standard Deviation
The standard deviation is the square root of the variance. Expressing variability in the original units of the data, it provides a more intuitive measure than the variance. A higher standard deviation indicates greater dispersion around the mean.
For population standard deviation (σ):
σ = √σ²
For sample standard deviation (s):
s = √s²
5. Mean Absolute Deviation (MAD)
The mean absolute deviation (MAD) measures the average absolute deviation of each data point from the mean. It’s less sensitive to outliers than the standard deviation because it uses absolute values instead of squared deviations.
6. Coefficient of Variation (CV)
The coefficient of variation (CV) is a relative measure of variability, expressed as a percentage. It's calculated as the ratio of the standard deviation to the mean:
CV = (σ / μ) * 100% (for population) CV = (s / x̄) * 100% (for sample)
The CV is useful for comparing the variability of datasets with different scales or units. A higher CV indicates greater relative variability.
Choosing the Right Measure of Variability
The selection of the appropriate measure of variability depends on several factors:
-
Data distribution: For datasets with a roughly symmetrical distribution, the standard deviation is often preferred. For skewed distributions or those with outliers, the IQR or MAD might be more appropriate.
-
Research question: The research question guides the choice of variability measure. If comparing variability across datasets with different scales is needed, the CV is ideal. If a simple, easy-to-understand measure is sufficient, the range might be adequate.
-
Robustness to outliers: The IQR and MAD are more robust to outliers than the range and standard deviation.
Variability in Different Contexts
Understanding variability is vital across numerous fields:
1. Finance
In finance, variability is crucial for risk management. The standard deviation of investment returns is a key measure of investment risk. Higher variability indicates greater uncertainty and potential for large losses or gains.
2. Healthcare
Variability in healthcare data can reveal inconsistencies in treatment outcomes or variations in patient response to medications. Analyzing variability helps improve healthcare practices and identify areas needing improvement.
3. Manufacturing
In manufacturing, variability in product dimensions or quality characteristics can lead to defects and inefficiencies. Statistical process control uses measures of variability to monitor production processes and ensure quality control.
Conclusion: The Importance of Understanding Variability
The variability of a statistic is a fundamental concept in data analysis. Understanding and appropriately measuring variability is essential for drawing reliable conclusions from data. The choice of measure depends on the data's characteristics, the research question, and the desired level of robustness to outliers. By effectively utilizing measures of dispersion, researchers and analysts can gain a clearer, more accurate understanding of the data and make more informed decisions. Ignoring variability can lead to flawed interpretations and inaccurate predictions. Therefore, mastering the various measures and their applications is crucial for anyone working with data.
Latest Posts
Latest Posts
-
Anatomy And Physiology 2 Exam 1 Quizlet
Mar 31, 2025
-
Fluid Electrolyte And Acid Base Balance Ati Quizlet
Mar 31, 2025
-
Functionalist Psychologists Focus On The Function Of Behavior And
Mar 31, 2025
-
Functions Of The Large Intestine Include Quizlet
Mar 31, 2025
-
An Interval Of An Ecg Is Quizlet
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about The Variability Of A Statistic Is Described By . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
