Which Function Is Shown In The Graph Below
Breaking News Today
Mar 31, 2025 · 6 min read
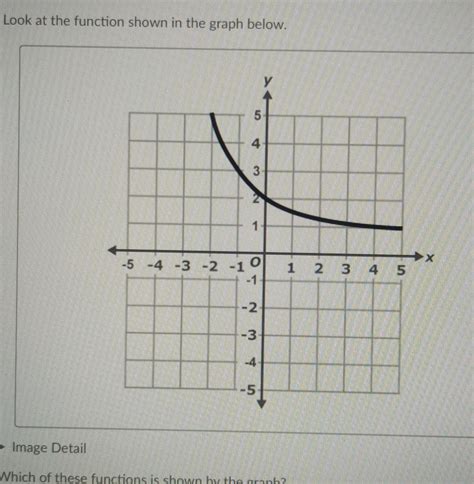
Table of Contents
Decoding the Graph: Identifying the Underlying Function
This article delves into the crucial skill of interpreting graphs and identifying the underlying mathematical function they represent. Analyzing graphs is a fundamental skill in various fields, from mathematics and physics to engineering and economics. Being able to accurately identify the type of function depicted in a graph – be it linear, quadratic, exponential, logarithmic, sinusoidal, or a combination thereof – is key to understanding the underlying relationships and making accurate predictions. Unfortunately, you haven't provided a graph. However, I will demonstrate the process using several example graphs, showing you the techniques and reasoning involved. This will equip you to analyze your graph effectively.
Understanding Different Function Types
Before we begin analyzing example graphs, let's refresh our understanding of common function types and their visual characteristics.
1. Linear Functions: These functions have the form y = mx + c, where 'm' represents the slope (rate of change) and 'c' represents the y-intercept (the point where the line crosses the y-axis). Graphically, linear functions appear as straight lines. A positive slope indicates an increasing function, while a negative slope indicates a decreasing function. A slope of zero means a horizontal line.
2. Quadratic Functions: These are functions of the form y = ax² + bx + c, where 'a', 'b', and 'c' are constants. Their graphs are parabolas – U-shaped curves. The value of 'a' determines the parabola's orientation: a positive 'a' results in a parabola that opens upwards, while a negative 'a' results in a parabola that opens downwards. The vertex of the parabola represents either the minimum or maximum value of the function.
3. Exponential Functions: These functions have the form y = abˣ, where 'a' is the initial value and 'b' is the base (growth or decay factor). If b > 1, the function represents exponential growth (a constantly increasing curve). If 0 < b < 1, the function represents exponential decay (a constantly decreasing curve approaching zero). Exponential functions increase or decrease at an increasingly rapid rate.
4. Logarithmic Functions: These are the inverse of exponential functions. They have the form y = logₐ(x), where 'a' is the base. Logarithmic functions show a slow increase as x increases. The graph approaches the y-axis asymptotically (gets infinitely close but never touches).
5. Sinusoidal Functions (Trigonometric Functions): These functions, like sine and cosine, have the form y = A sin(Bx + C) + D or y = A cos(Bx + C) + D, where A is the amplitude, B affects the period, C is the phase shift, and D is the vertical shift. Their graphs are waves that oscillate between a maximum and minimum value.
6. Polynomial Functions: These functions are sums of power functions of the form axⁿ, where 'n' is a non-negative integer. Quadratic functions are a specific type of polynomial function (n=2). Polynomial functions of higher degrees (n > 2) can have multiple turning points (local maxima and minima).
7. Rational Functions: These functions are ratios of two polynomial functions, y = P(x) / Q(x). They often have asymptotes (lines that the graph approaches but never touches) – vertical asymptotes where the denominator is zero and sometimes horizontal or oblique asymptotes.
Analyzing Example Graphs
Let's analyze some example graphs to illustrate the process of identifying the underlying function. Remember, these are simplified examples, and real-world graphs can be more complex.
Example 1: A Straight Line
Imagine a graph showing a straight line that passes through the points (0, 2) and (1, 5).
- Observation: The graph is a straight line, indicating a linear function.
- Slope Calculation: The slope (m) is calculated as (5 - 2) / (1 - 0) = 3.
- Y-intercept: The y-intercept (c) is 2 (the point where the line crosses the y-axis).
- Function: Therefore, the function is
y = 3x + 2.
Example 2: A Parabola Opening Upwards
Consider a graph resembling a U-shaped curve that passes through the points (-1, 2), (0, 1), and (1, 2).
- Observation: The graph is a parabola opening upwards, suggesting a quadratic function with a positive leading coefficient.
- Vertex: The vertex appears to be at (0,1).
- Points: Using the points, we can try to fit a quadratic equation of the form
y = ax² + bx + c. Substituting the points, we get a system of equations to solve for a, b, and c. Solving this (which involves some algebra) would yield the exact equation. However, a simpler approach here is to notice the parabola's symmetry. The parabola is symmetric around x = 0, meaning that it has the form y = ax² + 1. Using one of the points (1,2), we have 2 = a(1)² + 1, which gives a = 1. - Function: The likely function is therefore
y = x² + 1.
Example 3: An Exponential Growth Curve
Imagine a graph showing a curve that starts slowly, then increases rapidly as x increases. The curve never touches the x-axis.
- Observation: This indicates an exponential growth function.
- Shape: The constantly increasing rate of growth is the characteristic feature.
- Points: To find the precise equation, you would need to use the coordinates of points on the curve. For example, if the curve passes through (0, 1) and (1, 3), this suggests an exponential function of the form y = abˣ. Using the point (0,1), we get 1 = ab⁰ = a, so a=1. Using the point (1,3), we get 3 = 1*b¹, so b=3.
- Function: The function could be
y = 3ˣ.
Example 4: A Graph with Asymptotes
Consider a graph that approaches but never touches the x-axis and/or the y-axis.
- Observation: The presence of asymptotes is a strong indicator of a rational function or a logarithmic function.
- Asymptotes: Determining the location of the asymptotes is crucial. Vertical asymptotes are caused by values of x which would make the denominator of a rational function zero. Horizontal asymptotes indicate the behavior of the function as x goes to positive or negative infinity.
- Points: As in previous examples, points on the graph are needed to determine the precise equation.
Advanced Techniques and Considerations
- Data Fitting: For real-world data, specialized software or statistical techniques are often needed to fit functions to data points. These methods handle noise and uncertainty in the data. Tools like Excel, MATLAB, or Python libraries (like NumPy and SciPy) provide these capabilities.
- Transformation: Sometimes, it's useful to transform the data (e.g., by taking logarithms) to make the relationship clearer and easier to identify. This technique can linearize certain nonlinear functions, making analysis simpler.
- Multiple Functions: A graph could represent a piecewise function, combining different functions over different intervals. Identifying the type of function in each interval is then necessary.
Conclusion
Identifying the function shown in a graph is a crucial analytical skill. By carefully observing the shape of the graph, noting key features such as intercepts, slopes, asymptotes, and turning points, and utilizing appropriate mathematical techniques, you can determine the underlying function with a high degree of accuracy. Remember that having a strong grasp of various function types and their graphical representations is fundamental to this process. Practice is key—the more graphs you analyze, the more proficient you'll become at deciphering the mathematical relationships hidden within the visual data. While this article provides a comprehensive overview, remember that specific examples require detailed analysis, often involving algebraic manipulation and the use of data fitting techniques.
Latest Posts
Latest Posts
-
Provide An Appropriate Article And Noun For Each Picture
Apr 02, 2025
-
Pablo Y Mercedes Al Aeropuerto En Autobus
Apr 02, 2025
-
The Greek Words Demos And Kratis Together Mean
Apr 02, 2025
-
Essentials Of Radiographic Physics And Imaging Chapter 1
Apr 02, 2025
-
A Patients Refusal Of Ems Treatment Must Be
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about Which Function Is Shown In The Graph Below . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
